4.5.4 The Rules for the Lattice Grain Model

In order to keep the particle-particle interaction rules as simple as possible, all interparticle contacts, whether enduring contacts or true collisions, will be modelled as collisions. Collisions that model enduring contacts will transmit, in each time step, an impulse equal to the force of the enduring contact multiplied by the time step. The fact that collisions take place between particles on adjacent lattice nodes means that some particles may undergo up to six collisions in a time step. For simplicity, these collisions will be resolved as a series of binary collisions. The order in which these collisions are calculated at each lattice node, as well as the order in which the lattice nodes are scanned, is now an important consideration.

The rules of the Lattice Grain Model may be summarized as follows:

1. The particles reside on the nodes of a two-dimensional triangular lattice, obeying the exclusion principle that no node may have more than one particle.
2. Each particle has two components of velocity, which may take on any value. At the beginning of each time step, each particle's velocity is incremented due to the acceleration of gravity.
3. The size of each time step is set so that the fastest particle will travel one lattice spacing in that time step.
4. Two components of a ``position offset'' are maintained for each particle. This offset is incremented after the velocities in each time step according to gravitational acceleration and the particle's velocity:

   

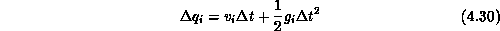
   where:

   

   Once the offset exceeds half the distance to the nearest lattice node, and that node is empty, the particle is moved to that node, and its offset is decremented appropriately. Also, in a collision, the component of the offset along the line connecting the centers of the colliding particles is set to zero.

5. The order in which the lattice is scanned is chosen so as not to create a coupling between the scan pattern and the particle motions. Thus, the particle position updates are done on every third lattice point of every third row, with this pattern being repeated nine times to cover all lattice sites.
6. Particle collisions are calculated assuming that they are smooth hard disks with a given coefficient of restitution. Particles on adjacent nodes are assumed to collide if their relative velocity is bringing them together. The following order has been adopted for evaluating possible collisions on odd time steps: 3b, 3c, 3f, 2f, 2c, 2b, 4b, 4c, 4f, 1f, 1c, 1b; and for even time steps: 1b, 1c, 1f, 4f, 4c, 4b, 2b, 2c, 2f, 3f, 3c, 3b (where the lattice numbers and collision directions are defined in Figure 4.25).
7. In order to incorporate a container, wall, or other barrier within these rules, a second type of particle is introduced-the wall particle. This particle is similar to the movable particles, and interacts with them through binary collisions (with a separately defined inelasticity), but is regarded as having infinite mass. To allow for the introduction of shearing motion from a wall (as in a Couette flow problem), the particles making up the wall are given a common constant velocity, which is used in the usual fashion for calculating the results of collisions. However, the position of the wall particles in the lattice remains fixed throughout the simulation.
8. Though a single particle does not accurately predict the trajectory of a single grain, we still regard each particle as representing one grain when we are extracting information from the simulation regarding the behavior of groups of grains. Thus, the size of one particle, as well as the spacing between lattice points, is taken to be one grain-diameter.

The transmission of ``static'' contact forces within a mass of grains (as in grains at rest in a gravitational field) is handled naturally within the above framework. Though a particle in a static mass of grains may be nominally at rest, its velocity may be nonzero (due to gravitational or pressure forces); and it will transmit the appropriate force (in the form of an impulse) to the particles under it by means of collisions. When these impulses are averaged over several time steps, the proper weights and pressures will emerge.

  
Figure 4.25: Definition of Lattice Numbers and Collision Directions