Symmetric Eigenproblems

   

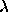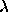Let A be a real symmetric   or complex Hermitian n-by-n matrix. A scalar is called an eigenvalue  and a nonzero column vector z the corresponding eigenvector  if . is always real when A is real symmetric or complex Hermitian.

The basic task of the symmetric eigenproblem routines is to compute values of 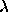and, optionally, corresponding vectors z for a given matrix A.

This computation proceeds in the following stages:

1. The real symmetric or complex Hermitian matrix A is reduced to real tridiagonal form   T. If A is real symmetric, the decomposition is with Q orthogonal and T symmetric tridiagonal. If A is complex Hermitian, the decomposition is with Q unitary and T, as before, real symmetric tridiagonal .
2. Eigenvalues and eigenvectors of the real symmetric tridiagonal matrix T are computed. If all eigenvalues and eigenvectors are computed, this process is equivalent to factorizing T as , where S is orthogonal and 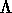is diagonal. The diagonal entries of 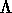are the eigenvalues of T, which are also the eigenvalues of A, and the columns of S are the eigenvectors of T; the eigenvectors of A are the columns of Z=QS, so that 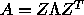( when A is complex Hermitian).

In the real case, the decomposition is computed by the routine PxSYTRD   (see table 3.8). The complex analogue of this routine is called PxHETRD.    The routine PxSYTRD (or PxHETRD) represents the matrix Q as a product of elementary reflectors, as described in section 3.4. The routine PxORMTR   (or in the complex case PxUNMTR)    is provided to multiply another matrix by Q without forming Q explicitly; this can be used to transform eigenvectors of T, computed by PxSTEIN, back to eigenvectors of A.     

The following routines compute eigenvalues  and eigenvectors  of T.

xSTEQR2

   This routine [77] is a modified version of LAPACK routine xSTEQR. It has fewer iterations than the LAPACK routine due to a modification in the look-ahead technique described in [77]. Some additional modifications allow each process to perform partial updates to matrix Q. This routine computes all eigenvalues and, optionally, eigenvectors of a symmetric tridiagonal matrix using the implicit QL or QR method.   

PxSTEBZ

   This routine uses bisection to compute some or all of the eigenvalues. Options provide for computing all the eigenvalues in a real interval or all the eigenvalues from the ith to the jth largest. It can be highly accurate but may be adjusted to run faster if lower accuracy is acceptable.

PxSTEIN

     Given accurate eigenvalues, this routine uses inverse iteration  to compute some or all of the eigenvectors.

Without any reorthogonalization, inverse iteration may produce vectors that have large dot products. To cure this, most implementations of inverse iteration such as LAPACK's xSTEIN reorthogonalize when eigenvalues differ by less than . As a result, the eigenvectors computed by xSTEIN are almost always orthogonal, but the increase in cost can result in work. On some rare examples, xSTEIN may still fail to deliver accurate answers; see [43, 44]. The orthogonalization done by PxSTEIN is limited by the amount of workspace provided; whenever it performs less reorthogonalization than xSTEIN, there is a danger that the dot products may not be satisfactory.

  
Table 3.8: Computational routines for the symmetric eigenproblem