To solve a linear least squares problem (3.1) when A is not of full rank, or the rank of A is in doubt, we can perform either a QR factorization with column pivoting or a singular value decomposition (see subsection 3.3.6).
The QR factorization with column pivoting is given by
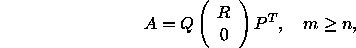
where Q and R are as before and P is a permutation matrix, chosen
(in general) so that
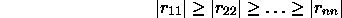
and moreover, for each k,
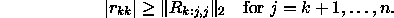
In exact arithmetic, if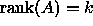 
, then the whole of the submatrix
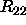in rows and columns k+1 to n
would be zero. In numerical computation, the aim must be to
determine an index k such that the leading submatrix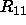 
in the first
k rows and columns is well conditioned and 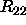is negligible:
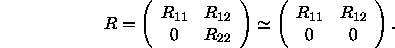
Then k is the effective rank of A.
See Golub and Van Loan [71]
for a further discussion of numerical rank determination.
The so-called basic solution to the linear least squares
problem (3.1) can be obtained from this factorization as
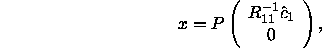
where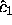 
consists of just the first k elements of 
.
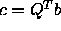The routine PxGEQPF computes the QR factorization with column pivoting but does not attempt to determine the rank of A. The matrix Q is represented in exactly the same way as after a call of PxGEQRF , and so the routines PxORGQR and PxORMQR can be used to work with Q (PxUNGQR and PxUNMQR if Q is complex).