Accounting for floating point errors





Next: Data Structures
Up: Stopping Criteria
Previous: Stopping when progress
The error bounds discussed in this section are subject to floating
point errors, most of which are innocuous, but which deserve some discussion.
The infinity norm 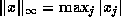 requires the fewest
floating point operations to compute, and cannot overflow or cause other
exceptions if the
requires the fewest
floating point operations to compute, and cannot overflow or cause other
exceptions if the 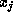 are themselves finite
are themselves finite . On the other hand, computing
. On the other hand, computing
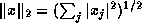 in the most straightforward manner
can easily overflow or lose accuracy to underflow even when the true result
is far from either the overflow or underflow thresholds. For this reason,
a careful implementation for computing
in the most straightforward manner
can easily overflow or lose accuracy to underflow even when the true result
is far from either the overflow or underflow thresholds. For this reason,
a careful implementation for computing 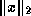 without this danger
is available (subroutine snrm2 in the BLAS [72] [144]),
but it is more expensive than computing
without this danger
is available (subroutine snrm2 in the BLAS [72] [144]),
but it is more expensive than computing 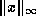 .
.
Now consider computing the residual 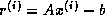 by forming the
matrix-vector product
by forming the
matrix-vector product 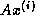 and then subtracting
and then subtracting 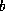 , all in floating
point arithmetic with relative precision
, all in floating
point arithmetic with relative precision  . A standard error
analysis shows that the error
. A standard error
analysis shows that the error 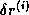 in the computed
in the computed 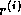 is bounded by
is bounded by
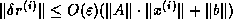 , where
, where
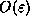 is typically bounded by
is typically bounded by 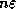 , and
usually closer to
, and
usually closer to 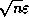 . This is why one should not choose
. This is why one should not choose
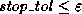 in Criterion 1, and why Criterion 2 may not
be satisfied by any method.
This uncertainty in the value of
in Criterion 1, and why Criterion 2 may not
be satisfied by any method.
This uncertainty in the value of
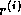 induces an uncertainty in the error
induces an uncertainty in the error 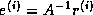 of
at most
of
at most
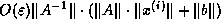 .
A more refined bound is that the error
.
A more refined bound is that the error 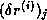 in the
in the
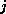 th component of
th component of 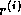 is bounded by
is bounded by 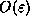 times the
times the 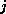 th component of
th component of
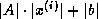 , or more tersely
, or more tersely
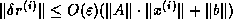 .
This means the uncertainty in
.
This means the uncertainty in 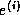 is really bounded by
is really bounded by
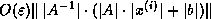 .
This last quantity can be estimated inexpensively provided solving systems
with
.
This last quantity can be estimated inexpensively provided solving systems
with  and
and 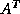 as coefficient matrices is inexpensive (see the last
paragraph of §
as coefficient matrices is inexpensive (see the last
paragraph of § ).
Both these bounds can be severe overestimates of the uncertainty in
).
Both these bounds can be severe overestimates of the uncertainty in 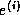 ,
but examples exist where they are attainable.
,
but examples exist where they are attainable.





Next: Data Structures
Up: Stopping Criteria
Previous: Stopping when progress
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
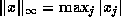 requires the fewest
floating point operations to compute, and cannot overflow or cause other
exceptions if the
requires the fewest
floating point operations to compute, and cannot overflow or cause other
exceptions if the 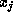 are themselves finite
are themselves finite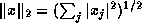 in the most straightforward manner
can easily overflow or lose accuracy to underflow even when the true result
is far from either the overflow or underflow thresholds. For this reason,
a careful implementation for computing
in the most straightforward manner
can easily overflow or lose accuracy to underflow even when the true result
is far from either the overflow or underflow thresholds. For this reason,
a careful implementation for computing 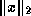 without this danger
is available (subroutine snrm2 in the BLAS [72] [144]),
but it is more expensive than computing
without this danger
is available (subroutine snrm2 in the BLAS [72] [144]),
but it is more expensive than computing 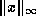 .
.
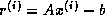 by forming the
matrix-vector product
by forming the
matrix-vector product 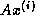 and then subtracting
and then subtracting 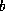 , all in floating
point arithmetic with relative precision
, all in floating
point arithmetic with relative precision  . A standard error
analysis shows that the error
. A standard error
analysis shows that the error 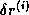 in the computed
in the computed 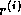 is bounded by
is bounded by
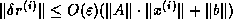 , where
, where
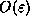 is typically bounded by
is typically bounded by 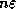 , and
usually closer to
, and
usually closer to 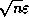 . This is why one should not choose
. This is why one should not choose
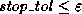 in Criterion 1, and why Criterion 2 may not
be satisfied by any method.
This uncertainty in the value of
in Criterion 1, and why Criterion 2 may not
be satisfied by any method.
This uncertainty in the value of
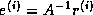 of
at most
of
at most
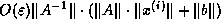 .
A more refined bound is that the error
.
A more refined bound is that the error 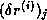 in the
in the
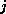 th component of
th component of 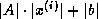 , or more tersely
, or more tersely
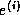 is really bounded by
is really bounded by
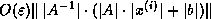 .
This last quantity can be estimated inexpensively provided solving systems
with
.
This last quantity can be estimated inexpensively provided solving systems
with  and
and 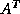 as coefficient matrices is inexpensive (see the last
paragraph of §
as coefficient matrices is inexpensive (see the last
paragraph of §