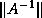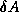 of
the coefficient matrix and
of
the coefficient matrix and 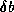 of the right hand side
of a linear system, such that the computed iterate
of the right hand side
of a linear system, such that the computed iterate 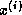 is the
solution of
is the
solution of 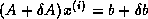 .
.
Stopping criterion: Since an iterative method computes successive
approximations to the solution of a linear system, a practical test is needed
to determine when to stop the iteration. Ideally this test would measure
the distance of the last iterate to the true solution, but this is not
possible. Instead, various other metrics are used, typically involving
the residual.
Forward error: The difference between a computed iterate and
the true solution of a linear system, measured in some vector norm.
Backward error: The size of perturbations 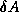 of
the coefficient matrix and
of
the coefficient matrix and 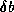 of the right hand side
of a linear system, such that the computed iterate
of the right hand side
of a linear system, such that the computed iterate 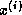 is the
solution of
is the
solution of 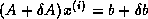 .
.
An iterative method produces a sequence  of vectors
converging to the vector
of vectors
converging to the vector  satisfying the
satisfying the 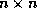 system
system 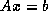 .
To be effective, a method must decide when to stop. A good stopping
criterion should
.
To be effective, a method must decide when to stop. A good stopping
criterion should
 is small
enough to stop,
is small
enough to stop,
For the user wishing to read as little as possible,
the following simple stopping criterion will likely be adequate.
The user must supply the quantities
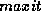 ,
, 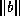 , stop_tol, and preferably also
, stop_tol, and preferably also  :
:
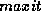 is the maximum number of iterations the algorithm
will be permitted to perform.
is the maximum number of iterations the algorithm
will be permitted to perform.
 is a norm of
is a norm of 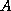 . Any reasonable
(order of magnitude) approximation of the absolute value of
the largest entry of the matrix
. Any reasonable
(order of magnitude) approximation of the absolute value of
the largest entry of the matrix 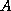 will do.
will do.
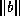 is a norm of
is a norm of 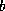 . Again, any
reasonable approximation of the
absolute value of the largest entry of
. Again, any
reasonable approximation of the
absolute value of the largest entry of 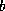 will do.
will do.
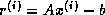 of the ultimate solution
of the ultimate solution
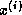 to be. One way to choose stop_tol is as the
approximate uncertainty in the entries of
to be. One way to choose stop_tol is as the
approximate uncertainty in the entries of 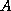 and
and 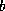 relative to
relative to
 and
and 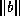 , respectively. For example, choosing stop_tol
, respectively. For example, choosing stop_tol
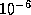 means that the user considers the entries of
means that the user considers the entries of 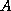 and
and 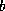 to have errors in the range
to have errors in the range 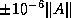 and
and 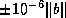 , respectively. The algorithm will compute
, respectively. The algorithm will compute  no more
accurately than its inherent uncertainty warrants. The user should
choose stop_tol less than one and greater than the machine
precision
no more
accurately than its inherent uncertainty warrants. The user should
choose stop_tol less than one and greater than the machine
precision  .
.Here is the algorithm:
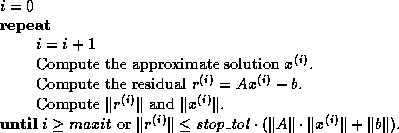
Note that if 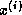 does not change much from step to step, which occurs
near convergence, then
does not change much from step to step, which occurs
near convergence, then 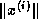 need not be recomputed.
If
need not be recomputed.
If  is not available, the stopping criterion may be replaced with
the generally stricter criterion
is not available, the stopping criterion may be replaced with
the generally stricter criterion
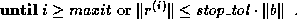
In either case, the final error bound is
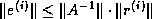 .
If an estimate of
.
If an estimate of 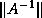 is available, one may also use the stopping
criterion
is available, one may also use the stopping
criterion

which guarantees that the relative error 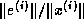 in the computed solution is bounded by stop_tol.
in the computed solution is bounded by stop_tol.
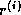 or
or 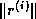 is not readily available
is not readily available