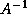 is the diagonal matrix
is the diagonal matrix 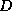 of
the reciprocals of the diagonal of
of
the reciprocals of the diagonal of 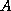 :
: 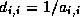 .
.
In block factorizations a pivot block is generally forced to be sparse, typically of banded form, and that we need an approximation to its inverse that has a similar structure. Furthermore, this approximation should be easily computable, so we rule out the option of calculating the full inverse and taking a banded part of it.
The simplest approximation to 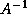 is the diagonal matrix
is the diagonal matrix 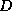 of
the reciprocals of the diagonal of
of
the reciprocals of the diagonal of 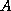 :
: 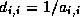 .
.
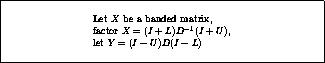
Figure: Algorithm for approximating the inverse of a banded matrix
Other possibilities were considered by
Axelsson and Eijkhout [15],
Axelsson and Polman [21],
Concus, Golub and Meurant [57],
Eijkhout and Vassilevski [90],
Kolotilina and Yeremin [141],
and Meurant [155]. One particular
example is given in figure ![]() . It has the attractive
theoretical property that, if the original matrix is symmetric
positive definite and a factorization with positive diagonal
. It has the attractive
theoretical property that, if the original matrix is symmetric
positive definite and a factorization with positive diagonal 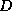 can
be made, the approximation to the inverse is again symmetric positive
definite.
can
be made, the approximation to the inverse is again symmetric positive
definite.
Banded approximations to the inverse of banded matrices have a
theoretical justification. In the context of partial differential
equations the diagonal blocks of the coefficient matrix are usually
strongly diagonally dominant. For such matrices, the elements of the
inverse have a size that is exponentially decreasing in their distance
from the main diagonal. See Demko, Moss and
Smith [65] for a general
proof, and Eijkhout and Polman [89] for a more detailed
analysis in the 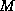 -matrix case.
-matrix case.