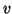diag(
diag(
span(
span(
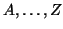 matrices
matrices
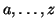 vectors
vectors
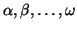 scalars
scalars
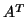 matrix transpose
matrix transpose
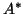 conjugate transpose of
conjugate transpose of 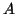
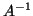 matrix inverse
matrix inverse
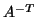 the inverse of
the inverse of 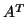
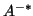 the inverse of
the inverse of 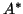
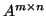 indicates that
indicates that 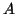 is
is 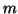 -by-
-by-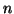
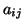 matrix element of
matrix element of 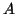
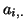
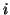 th row of matrix
th row of matrix 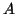
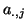
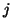 th column of matrix
th column of matrix 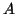
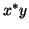 vector dot product
vector dot product
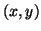 inner product, such as
inner product, such as 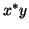
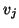 vector
vector 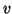 in the
in the 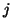 th iteration
th iteration
diag(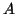 ) diagonal of matrix
) diagonal of matrix 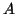
diag(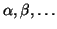 ) diagonal matrix constructed from scalars
) diagonal matrix constructed from scalars 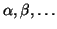
span(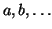 ) spanning space of vectors
) spanning space of vectors 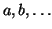
span(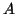 )
) 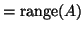 , subspace spanned by the columns of
, subspace spanned by the columns of 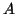
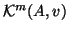 Krylov subspace
Krylov subspace 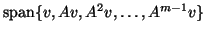
![$[x_1,x_2, \ldots ,x_m]$](img51.png) matrix whose
matrix whose 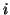 th column is
th column is 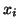
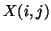
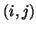 entry of
entry of 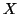
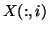 or
or 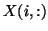
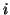 th column or row of
th column or row of 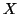
![$X(:,[2,3,5])$](img58.png) submatrix consisting of columns 2, 3, and 5 of
submatrix consisting of columns 2, 3, and 5 of 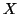
![$X([2,3,5],:)$](img59.png) submatrix consisting of rows 2, 3, and 5 of
submatrix consisting of rows 2, 3, and 5 of 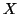
 ,
, 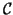 sets of real and complex numbers
sets of real and complex numbers
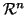 ,
, 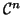 real and complex
real and complex 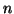 -spaces
-spaces
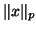 ,
, 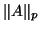 vector and matrix
vector and matrix 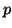 -norm
-norm
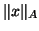 the ``
the ``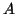 -norm,'' defined as
-norm,'' defined as 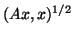
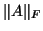 matrix Frobenius norm
matrix Frobenius norm
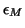 machine precision
machine precision
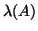 eigenvalues of
eigenvalues of 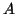
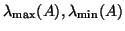 eigenvalues of
eigenvalues of 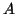 with maximum (resp., minimum) modulus
with maximum (resp., minimum) modulus
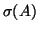 singular values of
singular values of 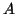
 largest and smallest singular values of
largest and smallest singular values of 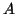
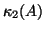 condition number of matrix
condition number of matrix 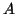 , defined as
, defined as 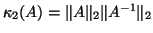
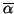 complex conjugate of the scalar
complex conjugate of the scalar 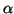
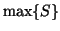 maximum value in set
maximum value in set 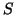
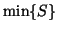 minimum value in set
minimum value in set 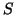
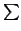 summation
summation
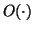 ``big-oh'' asymptotic bound
``big-oh'' asymptotic bound
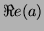 the real part of the complex number
the real part of the complex number 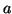
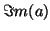 the imaginary part of the complex number
the imaginary part of the complex number 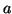
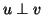 the vector
the vector 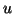 is orthogonal to the vector
is orthogonal to the vector