




Next: Singular Case
Up: Generalized Non-Hermitian Eigenproblems
Previous: Related Eigenproblems
Contents
Index
Example
We continue to use the example introduced in
§2.1 and
Figure 2.1.
We now consider the fully general case of nonzero masses 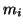 and damping constants
and damping constants 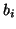 .
This leads to the equations
of motion
.
This leads to the equations
of motion
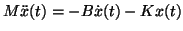 .
We solve them by changing variables to
.
We solve them by changing variables to
yielding
or
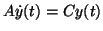 .
We solve this by substituting
.
We solve this by substituting
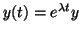 , where
, where 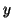 is
a constant vector and
is
a constant vector and  is a constant scalar to be determined.
This yields
is a constant scalar to be determined.
This yields
Thus 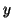 is an eigenvector
and
is an eigenvector
and  is an eigenvalue of the generalized nonsymmetric
eigenvalue problem.
is an eigenvalue of the generalized nonsymmetric
eigenvalue problem.
Susan Blackford
2000-11-20
![]() and damping constants
and damping constants ![]() .
This leads to the equations
of motion
.
This leads to the equations
of motion
![]() .
We solve them by changing variables to
.
We solve them by changing variables to