Specifying an Eigenproblem

The following eigenproblems are typical, because they arise naturally in applications and because we have algorithms for them:

1. Compute all the eigenvalues to some specified accuracy. This is typically done by computing the Schur form.
2. Compute the eigenvalues $\lambda_i$ in some region of the complex plane. This is typically done by computing an approximate right (and perhaps left) invariant subspace corresponding to eigenvalues in the desired region. The regions of the plane for which we have effective algorithms include
   1. the eigenvalues of closest to (or farthest from) a user-selected point $\mu$,
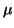   2. the eigenvalues of largest (or smallest) real (or imaginary) part,
   3. the eigenvalues closest to (or farthest from) any selected line or circle in the complex plane.

For each of these possibilities, the user can also compute a projection of the matrix on the specified invariant subspace; if the subspace is $k$-dimensional, then the projection is a $k$ by $k$ matrix whose eigendecomposition can be computed. The user can also compute the right (and perhaps left) eigenvectors in the computed invariant subspace. For the eigenvalues that are clustered together, the user may choose to compute the associated invariant subspace, since in this case the individual eigenvectors can be very ill-conditioned, while the invariant subspace may be less so. Finally, for any of these quantities, the user might also want to compute its condition number.

Even though we have effective algorithms for these problems, we cannot necessarily solve all large scale problems in an amount of time and space acceptable to all users.