Example

We continue to use the example introduced in §2.1 and Figure 2.1. We again consider the case with arbitrary masses $m_i>0$, and zero damping constants $b_i=0$. This simplifies the equations of motion to $M \ddot{x}(t) = -K x(t)$. As in §2.3.8 we solve the equations of motion by substituting $x(t) = e^{\lambda t} x$, where $x$ is a constant vector and $\lambda$ is a constant scalar to be determined. This leads to $Kx = -\lambda^2 Mx$. Letting $M = LL^T$, where the Cholesky factor $L = {\rm diag}( m_1^{1/2} ,\ldots, m_n^{1/2} )$, we see that we need to compute the eigenvalues of the symmetric tridiagonal matrix $\hat{K} = L^{-1}K L^{-T}$ shown in equation (2.2).

Now we note that the stiffness matrix $K$ can be factored as $K = BD^2B^T$, where $D = {\rm diag}(k_1^{1/2} ,\ldots, k_n^{1/2})$ and

$$B = \bmat{cccc} 1 & -1 & & \\ & \ddots & \ddots & \\ & & \ddots & -1 \\ & & & 1 \emat.$$

This lets us write

$$\begin{eqnarray*} \hat{K} & = & L^{-1} K L^{-T} = L^{-1} B D^2 B^T L^{-T} \nonum... ...^T L^{-T}) = (L^{-1} B D) \cdot (L^{-1} B D)^T \equiv GG^T. \end{eqnarray*}$$

Therefore, the singular values of the bidiagonal matrix

$$G = L^{-1}BD = \bmat{ccccc} \sqrt{k_1/m_1} & -\sqrt{k_2/m_1... ... \ddots & -\sqrt{k_n/m_{n-1}} \\ & & & & \sqrt{k_n/m_n}\emat$$

are the square roots of the eigenvalues of $\hat{K}$, and the left singular vectors of $G$ are the eigenvectors of $\hat{K}$.

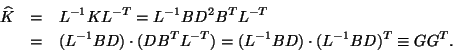
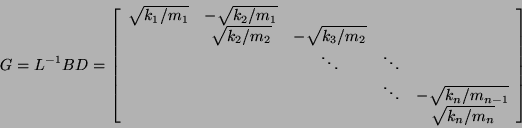
Bidiagonal matrices have particularly fast and efficient SVD algorithms.