




Next: Related Singular Value Problems
Up: Singular Value Decomposition J.
Previous: Conditioning
Contents
Index
Specifying a Singular Value Problem
The following problems are typical, both because they arise naturally
in applications and because we have good algorithms for them.
They correspond to the problems in §2.2.6.
- Compute all the singular values to some specified accuracy.
- Compute singular values
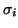 for some specified set of subscripts
for some specified set of subscripts
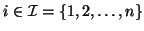 ,
including the special cases of the smallest
,
including the special cases of the smallest 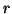 singular values
singular values
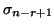 through
through
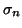 , and the largest
, and the largest 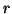 singular values
singular values 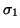 through
through 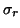 .
Again, the desired accuracy may be specified.
.
Again, the desired accuracy may be specified.
- Compute all the singular values within a given subset of the real axis,
such as the interval
![$[\alpha, \beta]$](img202.png) . Again, the desired accuracy may
be specified.
. Again, the desired accuracy may
be specified.
- Count all the singular values in the interval
![$[\alpha, \beta]$](img202.png) .
This does not require computing the singular values in
.
This does not require computing the singular values in
![$[\alpha, \beta]$](img202.png) ,
and so can be much cheaper.
,
and so can be much cheaper.
- Compute a certain number of singular values closest to a given value
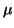 .
.
For each of these possibilities (except 4) the user can also compute the
corresponding singular vectors (left, right, or both).
For the singular values that are clustered together,
the user may choose to compute the associated singular subspace(s),
since in this case the individual singular vectors can be very
ill-conditioned,
while the singular subspace(s) may be less so.
Finally, for any of these quantities, the user might also want to
compute its condition number.
Even though we have effective algorithms for these problems,
we cannot necessarily achieve them all for large scale problems
in an amount of time and space acceptable to all users.





Next: Related Singular Value Problems
Up: Singular Value Decomposition J.
Previous: Conditioning
Contents
Index
Susan Blackford
2000-11-20