




Next: Parallelism J. Dongarra and
Up: Common Issues
Previous: Direct Solvers for Structured
Contents
Index
A Brief Survey of Iterative Linear Solvers
H. van der Vorst
In the context of eigenproblems it may be necessary to solve a
linear system, for instance, in the following situations:
- The Jacobi-Davidson methods require the (approximate) solution
of a linear correction equation.
- Inexact methods, like those discussed in Chapter 11, are
based on an approximate shift-and-invert step, for which a linear
system needs to be approximately solved.
- Given a good approximation for an eigenvalue, the corresponding
left or right eigenvector can be computed from a linear system
with the shifted matrix.
In all these cases, one has to solve a linear system with a shifted
matrix 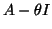 , sometimes embedded in projections as in the
Jacobi-Davidson methods. If such systems have to be solved accurately,
then direct (sparse) solvers may be considered first. Often one has
to solve more than one system with the same shifted matrix, which helps
to amortize large costs involved in making a sparse LU decomposition.
If the systems need not be solved accurately, or if direct solution
methods are too expensive, then iterative methods may be considered.
A set of popular iteration methods has been described in Templates for the Solution of Linear Systems [41].
Before we present a short overview, we warn the reader that the linear
systems related to eigenproblems usually have an indefinite matrix,
because of the involved shift. If the shift is near an exterior eigenvalue,
then this is not necessarily an obstacle in all cases, but there will
certainly be convergence problems for interior shifts. Also, when the
shift is very close to an eigenvalue, for instance, if one wants to determine
a left or right eigenvalue, then one should realize that iterative methods
have great difficulty solving almost singular systems. This holds in
particular for the situations of interest, where one is interested in the
(almost) singular directions, as is the case in inverse iteration for
left and right eigenvectors. It is commonly accepted that iterative
methods need efficient preconditioners in order to be attractive. This
is in particular the case for shifted matrices. Unfortunately, the
construction of effective preconditioners for indefinite matrices is
slippery ground to treat upon. See Chapter 11 for more on this.
, sometimes embedded in projections as in the
Jacobi-Davidson methods. If such systems have to be solved accurately,
then direct (sparse) solvers may be considered first. Often one has
to solve more than one system with the same shifted matrix, which helps
to amortize large costs involved in making a sparse LU decomposition.
If the systems need not be solved accurately, or if direct solution
methods are too expensive, then iterative methods may be considered.
A set of popular iteration methods has been described in Templates for the Solution of Linear Systems [41].
Before we present a short overview, we warn the reader that the linear
systems related to eigenproblems usually have an indefinite matrix,
because of the involved shift. If the shift is near an exterior eigenvalue,
then this is not necessarily an obstacle in all cases, but there will
certainly be convergence problems for interior shifts. Also, when the
shift is very close to an eigenvalue, for instance, if one wants to determine
a left or right eigenvalue, then one should realize that iterative methods
have great difficulty solving almost singular systems. This holds in
particular for the situations of interest, where one is interested in the
(almost) singular directions, as is the case in inverse iteration for
left and right eigenvectors. It is commonly accepted that iterative
methods need efficient preconditioners in order to be attractive. This
is in particular the case for shifted matrices. Unfortunately, the
construction of effective preconditioners for indefinite matrices is
slippery ground to treat upon. See Chapter 11 for more on this.
The currently most popular iterative methods belong to the class of
Krylov subspace methods. These methods construct approximations for
the solution from the so-called Krylov subspace.
The Krylov subspace
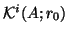 of dimension
of dimension 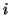 ,
associated with a linear
system
,
associated with a linear
system 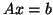 (where
(where  and
and 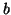 may be the preconditioned values, if
preconditioning is included) for a starting vector
may be the preconditioned values, if
preconditioning is included) for a starting vector 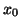 with residual
vector
with residual
vector 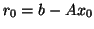 is defined as the subspace spanned by the
vectors {
is defined as the subspace spanned by the
vectors {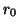 ,
, 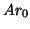 ,
,
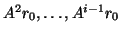 }.
}.
The different methods can be classified as follows:
- (a)
- If
 is symmetric positive definite, then the conjugate
gradient method [226] generates, using two-term recurrences,
the
is symmetric positive definite, then the conjugate
gradient method [226] generates, using two-term recurrences,
the 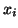 for which
for which
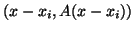 (the so-called
(the so-called  -norm or energy
norm) is minimized over all vectors in the current Krylov subspace
-norm or energy
norm) is minimized over all vectors in the current Krylov subspace
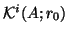 .
.
- (b)
- If
 is only symmetric but not positive definite, then
the Lanczos
[286] and the MINRES methods [350] may be
considered.
In MINRES, the
is only symmetric but not positive definite, then
the Lanczos
[286] and the MINRES methods [350] may be
considered.
In MINRES, the
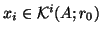 is determined for which
the 2-norm of the residual
(
is determined for which
the 2-norm of the residual
(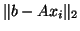 ) is minimized, while the Lanczos method leads to an
) is minimized, while the Lanczos method leads to an 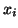 for which
for which 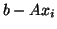 is perpendicular to the Krylov subspace.
is perpendicular to the Krylov subspace.
- (c)
- If
 is unsymmetric, it is in general not possible to determine
an optimal
is unsymmetric, it is in general not possible to determine
an optimal
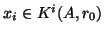 with short recurrences. This was proved
in [163]. However, with short recurrences as in conjugate
gradients (and MINRES), we can compute the
with short recurrences. This was proved
in [163]. However, with short recurrences as in conjugate
gradients (and MINRES), we can compute the
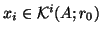 , for which
, for which
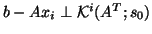 (usually, one selects
(usually, one selects 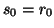 ). This leads to the bi-conjugate
gradient method [169].
A clever variant is quasi-minimal residual (QMR) [179], which
has smoother convergence behavior and is more
robust than bi-conjugate gradients.
). This leads to the bi-conjugate
gradient method [169].
A clever variant is quasi-minimal residual (QMR) [179], which
has smoother convergence behavior and is more
robust than bi-conjugate gradients.
- (d)
- If
 is unsymmetric, then we can compute
the
is unsymmetric, then we can compute
the
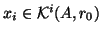 , for which the residual is minimized in
the Euclidean norm. This is done by the GMRES method [389].
This requires
, for which the residual is minimized in
the Euclidean norm. This is done by the GMRES method [389].
This requires 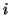 inner products at the
inner products at the 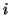 th iteration step,
as well as
th iteration step,
as well as 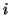 vector updates, which means that the iteration costs,
that come in addition to operations with
vector updates, which means that the iteration costs,
that come in addition to operations with  , grow linearly with
, grow linearly with 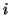 .
.
- (e)
- The operations with
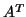 in the bi-conjugate gradient method can be replaced by operations
with
in the bi-conjugate gradient method can be replaced by operations
with  itself, by using the observation that
itself, by using the observation that
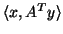 equals
equals
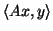 , where
, where
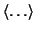 represents the inner-product computation.
Since the function of the multiplications by
represents the inner-product computation.
Since the function of the multiplications by 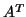 in bi-conjugate gradient serves
only to maintain the dual space to which residuals are orthogonalized,
the replacement of this operator by
in bi-conjugate gradient serves
only to maintain the dual space to which residuals are orthogonalized,
the replacement of this operator by  allows us to
expand the Krylov subspace and to find better approximations for
virtually the same costs per iteration as for bi-conjugate gradients.
This leads to so-called hybrid methods such as conjugate gradients squared [418],
Bi-CGSTAB [445], Bi-CGSTAB(
allows us to
expand the Krylov subspace and to find better approximations for
virtually the same costs per iteration as for bi-conjugate gradients.
This leads to so-called hybrid methods such as conjugate gradients squared [418],
Bi-CGSTAB [445], Bi-CGSTAB(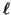 ) [409],
TFQMR [174], and hybrids of QMR [78].
) [409],
TFQMR [174], and hybrids of QMR [78].
- (f)
- For indefinite systems it may also be effective to apply
the conjugate gradient method for the normal equations
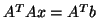 .
Carrying this out in a straight-forward manner may lead to numerical
instabilities, because
.
Carrying this out in a straight-forward manner may lead to numerical
instabilities, because 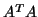 has a squared condition number. A clever
and robust implementation is provided in least squares QR [351].
has a squared condition number. A clever
and robust implementation is provided in least squares QR [351].
Many of these methods have been described in [41],
and software for them is available.
See this book's homepage, ETHOME, for guidelines on how to obtain the software.
For some methods, descriptions in templates style have been given
in [135]. That book also contains an overview on various
preconditioning approaches.





Next: Parallelism J. Dongarra and
Up: Common Issues
Previous: Direct Solvers for Structured
Contents
Index
Susan Blackford
2000-11-20
![]() of dimension
of dimension ![]() ,
associated with a linear
system
,
associated with a linear
system ![]() (where
(where ![]() and
and ![]() may be the preconditioned values, if
preconditioning is included) for a starting vector
may be the preconditioned values, if
preconditioning is included) for a starting vector ![]() with residual
vector
with residual
vector ![]() is defined as the subspace spanned by the
vectors {
is defined as the subspace spanned by the
vectors {![]() ,
, ![]() ,
,
![]() }.
}.