




Next: Direct Solvers for Band
Up: A Brief Survey of
Previous: A Brief Survey of
Contents
Index
Direct Solvers for Dense Matrices
There are two reasons to consider an iterative method
for dense matrices instead of using a transformation method:
- If one only wants a few eigenvalues and/or eigenvectors
near one or a few shifts
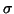 , it may be cheaper to use
shift-and-invert with an iterative scheme instead of a
transformation method. This is more likely true
with non-Hermitian matrices than Hermitian ones, for which the
transformation methods are faster.
, it may be cheaper to use
shift-and-invert with an iterative scheme instead of a
transformation method. This is more likely true
with non-Hermitian matrices than Hermitian ones, for which the
transformation methods are faster.
- When a matrix is not very sparse, or not very large, a dense
solver may be faster than a sparse solver.
The choice of dense solver depends on the mathematical structure of
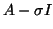 as follows:
as follows:
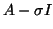 is Hermitian definite.
is Hermitian definite.- In this case Cholesky is the algorithm of choice.
It is implemented in LAPACK computational routines
xPOTRF to compute the factorization and
xPOTRS to solve using the factorization
(both are combined in LAPACK driver routine xPOSVX).
Versions for packed data storage are also available
(substitute PP for PO).
Cholesky is implemented in analogous ScaLAPACK routines
PxPOTRF, PxPOTRS, and PxPOSVX.
The factorization is in MATLAB as chol.
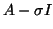 is Hermitian indefinite.
is Hermitian indefinite.- In this case Bunch-Kaufman is the algorithm of choice.
It is implemented in real (complex) LAPACK computational routines
xSYTRF(xHETRF) to compute the factorization and
xSYTRS(xHETRS) to solve using the factorization
(both are combined in LAPACK driver routine xSYSVX(xHESVX)).
Versions for packed data storage are also available
(substitute SP(HP) for SY(HE)).
It is not available in ScaLAPACK or MATLAB.
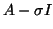 is non-Hermitian.
is non-Hermitian.- In this case Gaussian elimination is the algorithm of choice.
It is implemented in LAPACK computational routines
xGETRF to compute the factorization and
xGETRS to solve using the factorization
(both are combined in LAPACK driver routine xGESVX).
It is implemented in analogous ScaLAPACK routines
PxGETRF, PxGETRS, and PxGESVX.
The factorization is in MATLAB as lu.





Next: Direct Solvers for Band
Up: A Brief Survey of
Previous: A Brief Survey of
Contents
Index
Susan Blackford
2000-11-20
![]() as follows:
as follows: