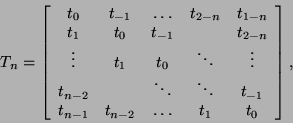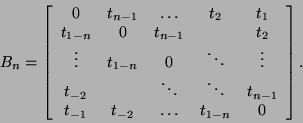Dense matrices that depend on ![]() parameters arise often in practice.
Examples of these matrices include
parameters arise often in practice.
Examples of these matrices include
Vandermonde:
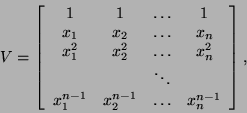
Toeplitz:
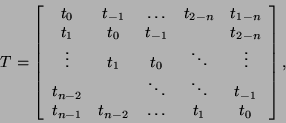
Hankel:
![]() ,
,
Cauchy:
![]() ,
and others [257].
,
and others [257].
These matrices and their inverses can be multiplied
by vectors in ![]() time, where
time, where
![]() , instead
of
, instead
of ![]() or
or ![]() time, depending on the structure.
This is particularly useful for using iterative solvers with
these matrices. The iterative solvers are also useful when solving systems
of the form
time, depending on the structure.
This is particularly useful for using iterative solvers with
these matrices. The iterative solvers are also useful when solving systems
of the form ![]() , where
, where ![]() and
and ![]() are both structured but
belong to different structured classes, or if
are both structured but
belong to different structured classes, or if ![]() is structured
and
is structured
and ![]() is banded or sparse, etc. Iterative methods are also useful for
solving block systems when the blocks are structured
matrices but belong to different structure classes with some
blocks also possibly being sparse. For example, the product
is banded or sparse, etc. Iterative methods are also useful for
solving block systems when the blocks are structured
matrices but belong to different structure classes with some
blocks also possibly being sparse. For example, the product
Vandermonde and inverses of Vandermonde matrices can be multiplied
by a vector in ![]() time [196,195].
The same is valid for
the Vandermonde-like and inverses of Vandermonde-like
matrices, where ``-like'' matrices are defined as
in § 10.3.4.
Matrix-vector multiplication for Toeplitz and Toeplitz-like
matrices takes
time [196,195].
The same is valid for
the Vandermonde-like and inverses of Vandermonde-like
matrices, where ``-like'' matrices are defined as
in § 10.3.4.
Matrix-vector multiplication for Toeplitz and Toeplitz-like
matrices takes
![]() time using the fast Fourier transform (FFT) [198].
The Cauchy matrix-vector product
time using the fast Fourier transform (FFT) [198].
The Cauchy matrix-vector product ![]() is equivalent
to the evaluation of the function
is equivalent
to the evaluation of the function
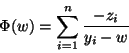
The rest of this section shows
how the ![]() matrix-vector multiplication works for
Toeplitz matrices [198].
For the other classes of structured matrices we refer the reader to
[196] and [195].
matrix-vector multiplication works for
Toeplitz matrices [198].
For the other classes of structured matrices we refer the reader to
[196] and [195].
A circulant matrix is a special Toeplitz matrix of the form
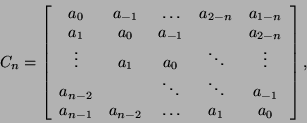
(1),
(2),
(3),
(4).
Now, if ![]() is a Toeplitz matrix
is a Toeplitz matrix