A $24 \times 21$ Singular Pencil in GUPTRI Form.

For completeness, we consider a pencil $A - \lambda B$ with all different types of structure blocks in its KCF:

$${\rm diag}(L_0, L_2, J_1(0), J_3(0), J_1(\alpha), J_1(\beta), J_1(\gamma), N_1, N_3, 2L_0^T, L_1^T, L_2^T, L_3^T).$$

Consequently, the GUPTRI form of this $24 \times 21$ pencil includes all types of diagonal blocks in (8.34) and (8.35). Since $A - \lambda B$ and the $6\times 8$ example have the same right singular structure and Jordan structure for the zero eigenvalue, they also have the same $A_r - \lambda B_r$ and $A_z - \lambda B_z$ (see above). The GUPTRI form of the Jordan structure of the infinity eigenvalue ( $A_i - \lambda B_i$) and the left singular structure ( $A_l - \lambda B_l$) are as follows:

$$A_{i} - \lambda B_{i} = \bmat{c\vert c\vert cc} {\bf z}& y ... ... x}& {\bf x}\\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \emat,$$

$$A_{l} - \lambda B_{l} = \bmat{c\vert cc\vert ccc} z & y & y... ... 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \emat.$$

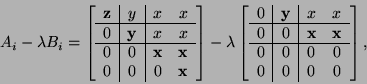
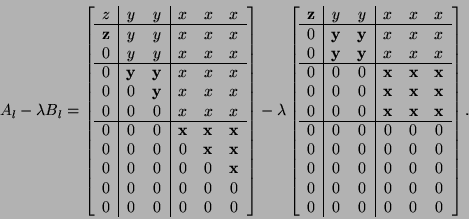
Since these forms are computed using the $LI$-staircase reduction, the block indices $n_i$ and $r_i$ start to count from the southeast corner. Now, superdiagonal blocks of $B_i$ and $B_l$ have full row rank and diagonal blocks of $A_i$ and $A_l$ have full column rank. In the following table, the structure indices for the $LI$-, $L$-, and $I$-staircase forms are summarized.

$i$	1	2	3	4
$n_i$	7	4	3	1
$r_i$	5	3	2	0

$i$	1	2	3	4
$n_i$	5	3	2	1
$r_i$	3	2	1	0

$i$	1	2	3	4
$n_i$	2	1	1	0
$r_i$	2	1	1	0

Finally, the block in the GUPTRI form corresponding to the finite and nonzero eigenvalues $\alpha, \beta$, and $\gamma$ has the following appearance:

$$A_{f} - \lambda B_{f} = \bmat{ccc} {\bf x}& x & x \\ 0 & ... ...{\bf x}& x & x \\ 0 & {\bf x}& x \\ 0 & 0 & {\bf x} \emat.$$

The diagonal elements in $A_f$ and $B_f$ are the eigenvalue pairs whose ratios are $\alpha, \beta$, and $\gamma$ (in any order).

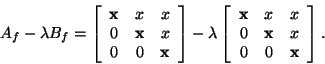
So far the description for computing the GUPTRI form has relied on infinite precision arithmetic. In the presence of roundoff the problem is regularized by allowing a deflation criterion for range/null space separations and thereby makes it possible to compute the GUPTRI form of a nearby matrix pencil.

This GUPTRI form is computed by a sequence of unitary equivalence transformations. The equivalence transformations are built from rank-revealing factorizations used to find orthonormal bases for different null spaces associated with the matrix pair.