Just as the Jordan canonical form (JCF) describes the
invariant subspaces and eigenvalues of a square matrix ![]() in full detail,
there is a Kronecker canonical form (KCF) which describes
the generalized eigenvalues and generalized eigenspaces of a
pencil
in full detail,
there is a Kronecker canonical form (KCF) which describes
the generalized eigenvalues and generalized eigenspaces of a
pencil ![]() in full detail.
In addition to Jordan blocks for finite and infinite eigenvalues,
the Kronecker form contains singular blocks corresponding to minimal
indices of a singular pencil (see below).
in full detail.
In addition to Jordan blocks for finite and infinite eigenvalues,
the Kronecker form contains singular blocks corresponding to minimal
indices of a singular pencil (see below).
The KCF of ![]() exhibits the fine structure elements,
including elementary divisors (Jordan blocks) and minimal indices
(singular blocks), and is defined as follows [187].
Suppose
exhibits the fine structure elements,
including elementary divisors (Jordan blocks) and minimal indices
(singular blocks), and is defined as follows [187].
Suppose
![]() .
Then there exist nonsingular
.
Then there exist nonsingular
![]() and
and
![]() such that
P^-1 (A - B)Q = Ã - B
diag( A_1 - B_1 , ..., A_b -
B_b ) ,
where
such that
P^-1 (A - B)Q = Ã - B
diag( A_1 - B_1 , ..., A_b -
B_b ) ,
where
![]() is
is
![]() .
We can partition the columns of
.
We can partition the columns of ![]() and
and ![]() into
blocks corresponding to the
into
blocks corresponding to the ![]() diagonal
blocks of
diagonal
blocks of
![]() :
:
![]() is a
is a ![]() block
corresponding to an infinite eigenvalue of multiplicity
block
corresponding to an infinite eigenvalue of multiplicity ![]() :
:
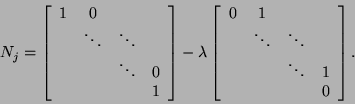
The
![]() and
and ![]() blocks together constitute the
regular structure of the pencil. All the
blocks together constitute the
regular structure of the pencil. All the
![]() are regular blocks if and only if
are regular blocks if and only if ![]() is a regular pencil.
is a regular pencil.
![]() denotes the eigenvalues of the regular part of
denotes the eigenvalues of the regular part of
![]() (counted with multiplicities) and is called the
spectrum of
(counted with multiplicities) and is called the
spectrum of ![]() .
.
The other two types of diagonal blocks are
L_j cccc
- & 1 & &
& & &
& & - & 1 and
L_j^T ccc
-& &
1 & &
& & -
& & 1 .
The
![]() block
block ![]() is called a singular block
of right (or column) minimal index
is called a singular block
of right (or column) minimal index ![]() .
It has a one-dimensional right null space,
.
It has a one-dimensional right null space,
![]() , for any
, for any ![]() , i.e.,
, i.e.,
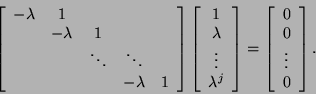
Similarly, the
![]() block
block ![]() is a singular block of left
(or row) minimal index
is a singular block of left
(or row) minimal index ![]() and has a
one-dimensional left null space for any
and has a
one-dimensional left null space for any ![]() .
The left and right singular blocks together constitute the
singular structure of the pencil and appear in the KCF if and only
if the pencil is singular.
The regular and singular structures define the Kronecker structure
of a singular pencil.
.
The left and right singular blocks together constitute the
singular structure of the pencil and appear in the KCF if and only
if the pencil is singular.
The regular and singular structures define the Kronecker structure
of a singular pencil.
We end this introductory description by briefly pointing to
the relationship between structure information
of the KCF and the GUPTRI form (8.28).
The block
![]() contains all information about
the right singular blocks and
contains all information about
the right singular blocks and
![]() contains all information about the left singular blocks.
The regular part corresponds to
contains all information about the left singular blocks.
The regular part corresponds to
![]() .
.