




Next: Transfer Residual Errors to
Up: Stability and Accuracy Assessments
Previous: Stability and Accuracy Assessments
Contents
Index
Let 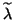 denote a computed eigenvalue of
denote a computed eigenvalue of  , and let
, and let
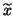 be its corresponding computed eigenvector, i.e.,
be its corresponding computed eigenvector, i.e.,
Sometimes, its corresponding left computed eigenvector
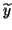 is also available:
is also available:
For simplicity,
we normalize the computed eigenvectors so that
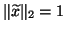 and
and
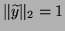 .
The residual vectors corresponding to the computed
eigenvalue
.
The residual vectors corresponding to the computed
eigenvalue 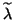 and right and left
computed eigenvectors
and right and left
computed eigenvectors 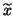 and
and 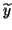 are defined as
are defined as
respectively.
We are interested in knowing the accuracy of the computed
eigenvalue 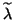 and eigenvectors
and eigenvectors 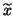 and
and
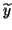 in terms of these residuals.
in terms of these residuals.
Susan Blackford
2000-11-20