




Next: Stability of .
Up: Orthogonal Deflating Transformation
Previous: Locking .
Contents
Index
If 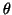 is ``unwanted" then we may
wish to remove
is ``unwanted" then we may
wish to remove 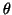 from the spectrum of the projected matrix
from the spectrum of the projected matrix 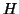 .
However, the implicit restart strategy using exact shifts
will sometimes fail to purge a converged unwanted Ritz value [294].
.
However, the implicit restart strategy using exact shifts
will sometimes fail to purge a converged unwanted Ritz value [294].
We shall use (7.21) to purge an unwanted but converged Ritz value.
In this case, a left eigenvector 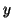 is needed with
is needed with
Now, when we apply
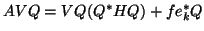 , we obtain
, we obtain
where 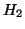 is upper Hessenberg. Here,
is upper Hessenberg. Here, 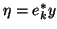 as before, but
there is no requirement that
as before, but
there is no requirement that 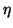 be small. The desired purging amounts
to simply discarding the first column on both sides of this equation.
We are then left with
be small. The desired purging amounts
to simply discarding the first column on both sides of this equation.
We are then left with
No error other than an acceptable level
of roundoff will be introduced through this purging process.
Moreover, there is no requirement that 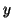 be an accurate left
eigenvector for
be an accurate left
eigenvector for 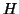 . It is only necessary that the
residual
. It is only necessary that the
residual
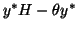 be small.
be small.





Next: Stability of .
Up: Orthogonal Deflating Transformation
Previous: Locking .
Contents
Index
Susan Blackford
2000-11-20
![]() is needed with
is needed with