




Next: Deflation
Up: Arnoldi Method Y. Saad
Previous: Variants
Contents
Index
Explicit Restarts
As was mentioned earlier, the standard implementations of the Arnoldi
method are limited by their high storage and computational
requirements as 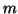 increases. Suppose that we are interested in only
one eigenvalue/eigenvector of
increases. Suppose that we are interested in only
one eigenvalue/eigenvector of  , namely, the eigenvalue of largest
real part of
, namely, the eigenvalue of largest
real part of  . Then one way to circumvent the difficulty is to
restart the algorithm. After a run with
. Then one way to circumvent the difficulty is to
restart the algorithm. After a run with 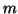 Arnoldi vectors,
we compute the approximate eigenvector and use it as an initial
vector for the next run with the Arnoldi method. This process, which is
the simplest of this kind, is iterated to convergence to compute
one eigenpair. For computing other eigenpairs, and for improving
the efficiency of the process, a number of strategies have been
developed, which are somewhat related. These include
deflation procedures briefly discussed in the next section,
and the implicit restarting strategy described in §7.6.
Arnoldi vectors,
we compute the approximate eigenvector and use it as an initial
vector for the next run with the Arnoldi method. This process, which is
the simplest of this kind, is iterated to convergence to compute
one eigenpair. For computing other eigenpairs, and for improving
the efficiency of the process, a number of strategies have been
developed, which are somewhat related. These include
deflation procedures briefly discussed in the next section,
and the implicit restarting strategy described in §7.6.

Susan Blackford
2000-11-20

