




Next: Subspace Iteration
Up: Single- and Multiple-Vector Iterations
Previous: Power Method
Contents
Index
Inverse Iteration
Inverse iteration, described in Algorithm 4.2,
can also be used to solve the
NHEP without any apparent change.

As in the Hermitian case, assume that 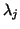 and
and
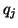 are an eigenvalue and eigenvector pair of
are an eigenvalue and eigenvector pair of  so that
so that
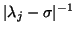 is the largest eigenvalue of
is the largest eigenvalue of
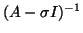 in magnitude. The inverse power method
converges if the starting vector
in magnitude. The inverse power method
converges if the starting vector
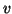 is not perpendicular to
is not perpendicular to 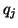 . The
convergence rate is
. The
convergence rate is
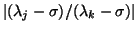 , where
, where 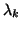 is an eigenvalue of
is an eigenvalue of
 such that
such that
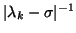 is the second
largest eigenvalue of
is the second
largest eigenvalue of
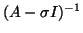 in magnitude.
in magnitude.
In general, inverse iteration tends to have
much more rapid convergence than the power method if
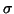 is chosen to be very close to a desired
eigenvalue. However, inverse iteration does require a
factorization of the matrix
is chosen to be very close to a desired
eigenvalue. However, inverse iteration does require a
factorization of the matrix 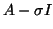 , making it less
attractive when this factorization is expensive.
, making it less
attractive when this factorization is expensive.
Susan Blackford
2000-11-20

![]() is chosen to be very close to a desired
eigenvalue. However, inverse iteration does require a
factorization of the matrix
is chosen to be very close to a desired
eigenvalue. However, inverse iteration does require a
factorization of the matrix ![]() , making it less
attractive when this factorization is expensive.
, making it less
attractive when this factorization is expensive.