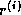 or
or  is not readily available
is not readily available
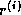 or
or  is not readily available
is not readily available
It is possible to design an iterative algorithm for which
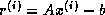 or
or  is not directly available,
although this is not the case for any algorithms in this book.
For completeness, however, we discuss stopping criteria in this case.
is not directly available,
although this is not the case for any algorithms in this book.
For completeness, however, we discuss stopping criteria in this case.
For example, if ones ``splits'' 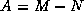 to get the iterative
method
to get the iterative
method  , then the
natural residual to compute is
, then the
natural residual to compute is
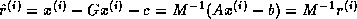 .
In other words, the residual
.
In other words, the residual  is the same as the residual of the
preconditioned system
is the same as the residual of the
preconditioned system 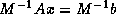 . In this case, it is
hard to interpret
. In this case, it is
hard to interpret  as a backward error for the original system
as a backward error for the original system
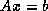 , so we may instead derive a forward error bound
, so we may instead derive a forward error bound
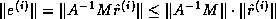 .
Using this as a stopping criterion requires an estimate of
.
Using this as a stopping criterion requires an estimate of
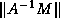 .
In the case of methods based on
splitting
.
In the case of methods based on
splitting 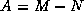 , we have
, we have 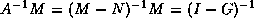 ,
and
,
and  .
.
Another example is an implementation of the preconditioned conjugate
gradient algorithm which computes 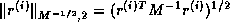 instead of
instead of 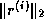 (the
implementation in this book computes the latter). Such an
implementation could use the stopping criterion
(the
implementation in this book computes the latter). Such an
implementation could use the stopping criterion 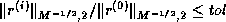 as in Criterion 5. We
may also use it to get the forward error bound
as in Criterion 5. We
may also use it to get the forward error bound 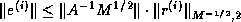 , which could also
be used in a stopping criterion.
, which could also
be used in a stopping criterion.