Left and right preconditioning





Next: Jacobi Preconditioning
Up: The why and
Previous: Cost trade-off
The above transformation of the linear system 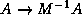 is often not what is used in practice. For instance, the matrix
is often not what is used in practice. For instance, the matrix 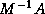 is
not symmetric, so, even if
is
not symmetric, so, even if 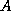 and
and 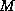 are, the conjugate gradients
method is not immediately applicable to this system. The method as
described in figure
are, the conjugate gradients
method is not immediately applicable to this system. The method as
described in figure  remedies this by employing the
remedies this by employing the
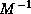 -inner product for orthogonalization of the residuals. The
theory of the cg method is then applicable again.
-inner product for orthogonalization of the residuals. The
theory of the cg method is then applicable again.
All cg-type methods in this book, with the exception of QMR, have been
derived with such a combination of preconditioned iteration matrix
and correspondingly changed inner product.
Another way of deriving the preconditioned conjugate gradients method
would be to split the preconditioner as 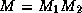 and
to transform the system as
and
to transform the system as
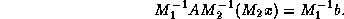
If 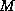 is symmetric and
is symmetric and 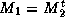 , it is obvious that we now have a
method with a symmetric iteration matrix, hence the conjugate
gradients method can be applied.
, it is obvious that we now have a
method with a symmetric iteration matrix, hence the conjugate
gradients method can be applied.
Remarkably, the splitting of 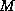 is in practice not needed.
By rewriting the steps of the method (see for
instance Axelsson and
Barker [pgs. 16,29]AxBa:febook or Golub and
Van Loan [.3]GoVL:matcomp) it
is usually possible to reintroduce a computational step
is in practice not needed.
By rewriting the steps of the method (see for
instance Axelsson and
Barker [pgs. 16,29]AxBa:febook or Golub and
Van Loan [.3]GoVL:matcomp) it
is usually possible to reintroduce a computational step

that is, a step that applies the preconditioner in its entirety.
There is a different approach to preconditioning, which is much easier
to derive. Consider again the system.
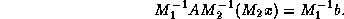
The matrices 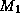 and
and 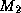 are called the left- and right preconditioners , respectively, and we can simply apply an
unpreconditioned iterative method to this system. Only two additional
actions
are called the left- and right preconditioners , respectively, and we can simply apply an
unpreconditioned iterative method to this system. Only two additional
actions 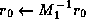 before the iterative process and
before the iterative process and
 after are necessary.
after are necessary.
Thus we arrive at the following schematic for deriving a left/right
preconditioned iterative method from any of the symmetrically
preconditioned methods in this book.
- Take a preconditioned iterative method, and replace every
occurrence of
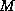 by
by 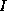 .
.
- Remove any vectors from the algorithm that have become
duplicates in the previous step.
- Replace every occurrence of
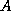 in the method by
in the method by  .
.
- After the calculation of the initial residual, add the step

- At the end of the method, add the step

where  is the final calculated solution.
is the final calculated solution.
It should be noted that such methods cannot be made to reduce to the
algorithms given in section  by such
choices as
by such
choices as 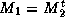 or
or 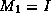 .
.





Next: Jacobi Preconditioning
Up: The why and
Previous: Cost trade-off
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
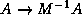 is often not what is used in practice. For instance, the matrix
is often not what is used in practice. For instance, the matrix 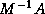 is
not symmetric, so, even if
is
not symmetric, so, even if 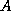 and
and 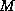 are, the conjugate gradients
method is not immediately applicable to this system. The method as
described in figure
are, the conjugate gradients
method is not immediately applicable to this system. The method as
described in figure 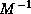 -inner product for orthogonalization of the residuals. The
theory of the cg method is then applicable again.
-inner product for orthogonalization of the residuals. The
theory of the cg method is then applicable again.
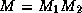 and
to transform the system as
and
to transform the system as
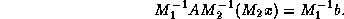
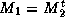 , it is obvious that we now have a
method with a symmetric iteration matrix, hence the conjugate
gradients method can be applied.
, it is obvious that we now have a
method with a symmetric iteration matrix, hence the conjugate
gradients method can be applied.

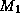 and
and 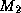 are called the left-
are called the left-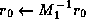 before the iterative process and
before the iterative process and
 after are necessary.
after are necessary.
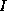 .
.
 .
.


 is the final calculated solution.
is the final calculated solution.
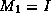 .
.