Quasi-Minimal Residual (QMR)





Next: Convergence
Up: Nonstationary Iterative Methods
Previous: Implementation
The BiConjugate Gradient method often displays rather irregular
convergence behavior. Moreover, the implicit
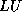 decomposition of the
reduced tridiagonal system may not exist, resulting in breakdown of the algorithm. A related algorithm, the
Quasi-Minimal Residual method of Freund and
Nachtigal [102], [103]
attempts to overcome
these problems. The main idea behind this algorithm is to solve the
reduced tridiagonal system in a least squares sense, similar to the
approach followed in GMRES.
Since the constructed basis for the
Krylov subspace
is bi-orthogonal , rather than orthogonal as in GMRES,
the obtained solution is viewed as a quasi-minimal residual solution,
which explains the name. Additionally, QMR uses look-ahead techniques
to avoid breakdowns in the underlying Lanczos process, which makes it
more robust than BiCG.
decomposition of the
reduced tridiagonal system may not exist, resulting in breakdown of the algorithm. A related algorithm, the
Quasi-Minimal Residual method of Freund and
Nachtigal [102], [103]
attempts to overcome
these problems. The main idea behind this algorithm is to solve the
reduced tridiagonal system in a least squares sense, similar to the
approach followed in GMRES.
Since the constructed basis for the
Krylov subspace
is bi-orthogonal , rather than orthogonal as in GMRES,
the obtained solution is viewed as a quasi-minimal residual solution,
which explains the name. Additionally, QMR uses look-ahead techniques
to avoid breakdowns in the underlying Lanczos process, which makes it
more robust than BiCG.

Figure: The Preconditioned Quasi Minimal Residual Method
without Look-ahead
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
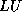 decomposition of the
reduced tridiagonal system may not exist, resulting in breakdown of the algorithm. A related algorithm, the
Quasi-Minimal Residual method of Freund and
Nachtigal [102], [103]
attempts to overcome
these problems. The main idea behind this algorithm is to solve the
reduced tridiagonal system in a least squares sense, similar to the
approach followed in GMRES.
Since the constructed basis for the
Krylov subspace
is bi-orthogonal , rather than orthogonal as in GMRES,
the obtained solution is viewed as a quasi-minimal residual solution,
which explains the name. Additionally, QMR uses look-ahead techniques
to avoid breakdowns in the underlying Lanczos process, which makes it
more robust than BiCG.
decomposition of the
reduced tridiagonal system may not exist, resulting in breakdown of the algorithm. A related algorithm, the
Quasi-Minimal Residual method of Freund and
Nachtigal [102], [103]
attempts to overcome
these problems. The main idea behind this algorithm is to solve the
reduced tridiagonal system in a least squares sense, similar to the
approach followed in GMRES.
Since the constructed basis for the
Krylov subspace
is bi-orthogonal , rather than orthogonal as in GMRES,
the obtained solution is viewed as a quasi-minimal residual solution,
which explains the name. Additionally, QMR uses look-ahead techniques
to avoid breakdowns in the underlying Lanczos process, which makes it
more robust than BiCG.
