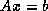If a system of linear equations 
has a nonsymmetric, possibly
indefinite (but nonsingular), coefficient matrix, one obvious attempt
at a solution is to apply Conjugate Gradient to a related symmetric positive definite system,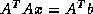 
. While
this approach is easy to understand and code, the convergence speed of
the Conjugate Gradient method now depends on the square of the
condition number of the original coefficient matrix. Thus the
rate of convergence of the CG procedure on the normal equations may be slow.
Several proposals have been made to improve the numerical stability of this method. The best known is by Paige and Saunders [169] and is based upon applying the Lanczos method to the auxiliary system
A clever execution of this scheme delivers the factors 
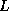and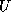 
of the 
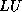-decomposition of the tridiagonal matrix that would
have been computed by carrying out the Lanczos procedure with 
.
Another means for improving the numerical stability of this normal
equations approach is suggested by Björck and Elfving in [34].
The observation that the matrix is used in the construction of
the iteration coefficients through an inner product like 
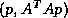leads to the suggestion that such an inner product
be replaced by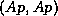 
.