Theory





Next: Convergence
Up: Conjugate Gradient Method
Previous: Conjugate Gradient Method
The unpreconditioned conjugate gradient method constructs the 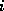 th
iterate
th
iterate  as an element of
as an element of
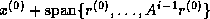 so that
so that
 is minimized , where
is minimized , where
 is the exact solution of
is the exact solution of 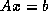 . This minimum is guaranteed
to exist in general only if
. This minimum is guaranteed
to exist in general only if 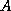 is symmetric positive definite. The
preconditioned version of the method uses a different subspace for
constructing the iterates, but it satisfies the same minimization
property, although over this different subspace. It requires in
addition that the preconditioner
is symmetric positive definite. The
preconditioned version of the method uses a different subspace for
constructing the iterates, but it satisfies the same minimization
property, although over this different subspace. It requires in
addition that the preconditioner 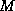 is symmetric and positive
definite.
is symmetric and positive
definite.
The above minimization of the error is equivalent to the residuals
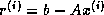 being
being 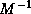 orthogonal (that is,
orthogonal (that is, 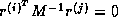 if
if 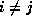 ). Since for symmetric
). Since for symmetric 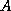 an orthogonal basis for the Krylov subspace
an orthogonal basis for the Krylov subspace
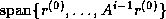 can be
constructed with only three-term recurrences , such a recurrence also
suffices for generating the residuals. In the Conjugate
Gradient method two coupled two-term recurrences are used; one that
updates residuals using a search direction vector, and one updating
the search direction with a newly computed residual.
This makes the
Conjugate Gradient Method quite attractive computationally.
can be
constructed with only three-term recurrences , such a recurrence also
suffices for generating the residuals. In the Conjugate
Gradient method two coupled two-term recurrences are used; one that
updates residuals using a search direction vector, and one updating
the search direction with a newly computed residual.
This makes the
Conjugate Gradient Method quite attractive computationally.
Krylov sequence: For a given matrix 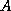 and vector
and vector  , the
sequence of vectors
, the
sequence of vectors 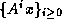 , or a finite initial part
of this sequence.
Krylov subspace: The subspace spanned by a Krylov sequence.
, or a finite initial part
of this sequence.
Krylov subspace: The subspace spanned by a Krylov sequence.
There is a close relationship between the Conjugate Gradient method
and the Lanczos method for determining eigensystems, since both are
based on the construction of an orthogonal basis for the Krylov
subspace, and a similarity transformation of the coefficient matrix to
tridiagonal form. The coefficients computed during
the CG iteration then arise from the 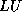 factorization of this
tridiagonal matrix.
From the CG iteration one can reconstruct the Lanczos process, and vice versa;
see Paige and Saunders [168]
and Golub and Van Loan [.2.6]GoVL:matcomp.
This relationship can be exploited to obtain relevant information
about the eigensystem of the (preconditioned) matrix
factorization of this
tridiagonal matrix.
From the CG iteration one can reconstruct the Lanczos process, and vice versa;
see Paige and Saunders [168]
and Golub and Van Loan [.2.6]GoVL:matcomp.
This relationship can be exploited to obtain relevant information
about the eigensystem of the (preconditioned) matrix 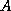 ;
see §
;
see § .
.





Next: Convergence
Up: Conjugate Gradient Method
Previous: Conjugate Gradient Method
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
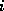 th
iterate
th
iterate  as an element of
as an element of
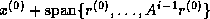 so that
so that
 is minimized , where
is minimized , where
 is the exact solution of
is the exact solution of 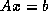 . This minimum is guaranteed
to exist in general only if
. This minimum is guaranteed
to exist in general only if 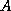 is symmetric positive definite. The
preconditioned version of the method uses a different subspace for
constructing the iterates, but it satisfies the same minimization
property, although over this different subspace. It requires in
addition that the preconditioner
is symmetric positive definite. The
preconditioned version of the method uses a different subspace for
constructing the iterates, but it satisfies the same minimization
property, although over this different subspace. It requires in
addition that the preconditioner 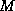 is symmetric and positive
definite.
is symmetric and positive
definite.
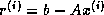 being
being 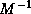 orthogonal (that is,
orthogonal (that is, 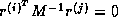 if
if 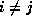 ). Since for symmetric
). Since for symmetric 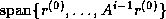 can be
can be , the
sequence of vectors
, the
sequence of vectors 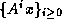 , or a finite initial part
of this sequence.
Krylov subspace: The subspace spanned by a Krylov sequence.
, or a finite initial part
of this sequence.
Krylov subspace: The subspace spanned by a Krylov sequence.
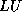 factorization of this
tridiagonal matrix.
From the CG iteration one can reconstruct the Lanczos process, and vice versa;
see Paige and Saunders
factorization of this
tridiagonal matrix.
From the CG iteration one can reconstruct the Lanczos process, and vice versa;
see Paige and Saunders