
Most iterative methods depend on spectral properties of the coefficient matrix, for instance some require the eigenvalues to be in the right half plane. A class of methods without this limitation is that of row projection methods (see Björck and Elfving [34], and Bramley and Sameh [38]). They are based on a block row partitioning of the coefficient matrix

and iterative application of orthogonal projectors
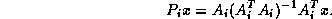
These methods have good parallel properties and seem to be robust in handling nonsymmetric and indefinite problems.
Row projection methods can be used as
preconditioners in the conjugate gradient method. In that case, there
is a theoretical connection with the conjugate gradient method on the
normal equations (see §![]() ).
).