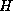
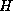
Given 
, it has been observed empirically (see Gropp and
Keyes [111]) that there often exists an optimal value of
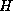which minimizes the total computational time for solving the problem.
A small 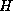provides a better, but more expensive, coarse grid
approximation, and requires solving more, but smaller, subdomain
solves. A large 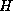has the opposite effect. For model problems, the
optimal 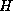can be determined for both sequential and parallel
implementations (see Chan and Shao [53]). In
practice, it may pay to determine a near optimal value of
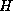empirically if the preconditioner is to be re-used many times.
However, there
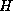may also be geometric constraints on the range of values that can
take.