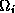 is extended to a
larger substructure
is extended to a
larger substructure 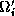 containing
containing 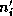 internal vertices and all the
triangles
internal vertices and all the
triangles 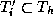 , within a distance
, within a distance 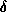 from
from
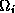 , where
, where 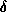 refers to the amount of overlap.
refers to the amount of overlap.
In this approach, each substructure 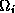 is extended to a
larger substructure
is extended to a
larger substructure 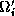 containing
containing 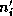 internal vertices and all the
triangles
internal vertices and all the
triangles 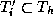 , within a distance
, within a distance 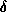 from
from
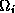 , where
, where 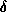 refers to the amount of overlap.
refers to the amount of overlap.
Let 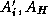 denote the the discretizations
of (
denote the the discretizations
of (![]() ) on the subdomain
triangulation
) on the subdomain
triangulation 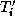 and the coarse triangulation
and the coarse triangulation 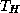 respectively.
respectively.
Let 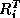 denote the extension operator which extends (by zero) a
function on
denote the extension operator which extends (by zero) a
function on 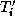 to
to 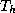 and
and
 the corresponding pointwise restriction operator.
Similarly, let
the corresponding pointwise restriction operator.
Similarly, let 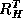 denote the interpolation operator
which maps a function on the coarse grid
denote the interpolation operator
which maps a function on the coarse grid 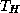 onto the fine
grid
onto the fine
grid 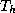 by piecewise linear interpolation
and
by piecewise linear interpolation
and 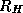 the corresponding weighted restriction operator.
the corresponding weighted restriction operator.
With these notations, the Additive Schwarz Preconditioner 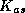 for
the system
for
the system 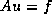 can be compactly described as:
can be compactly described as:
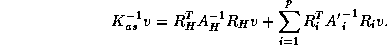
Note that the right hand side can be computed using

subdomain solves using the

's, plus a coarse grid solve using

, all of which can be computed in parallel. Each term

should be evaluated in three steps: (1) Restriction:

, (2) Subdomain solves for

:

, (3) Interpolation:

. The coarse grid solve is handled in the same manner.
The theory of Dryja and Widlund [76] shows that the condition number of

is bounded independently of both the coarse grid size

and the fine grid size

, provided there is ``sufficient'' overlap between

and

(essentially it means that the ratio

of the distance

of the boundary

to

should be uniformly bounded from below as

.) If the coarse grid solve term is left out, then the condition number grows as

, reflecting the lack of global coupling provided by the coarse grid.
For the purpose of implementations, it is often useful to interpret the definition of

in matrix notation. Thus the decomposition of

into

's corresponds to partitioning of the components of the vector

into

overlapping groups of index sets

's, each with

components. The

matrix

is simply a principal submatrix of

corresponding to the index set

.

is a

matrix defined by its action on a vector

defined on

as:

if

but is zero otherwise. Similarly, the action of its transpose

forms an

-vector by picking off the components of

corresponding to

. Analogously,

is an

matrix with entries corresponding to piecewise linear interpolation and its transpose can be interpreted as a weighted restriction matrix. If

is obtained from

by nested refinement, the action of

can be efficiently computed as in a standard multigrid algorithm. Note that the matrices

are defined by their actions and need not be stored explicitly.
We also note that in this algebraic formulation, the preconditioner

can be extended to any matrix

, not necessarily one arising from a discretization of an elliptic problem. Once we have the partitioning index sets

's, the matrices

are defined. Furthermore, if

is positive definite, then

is guaranteed to be nonsingular. The difficulty is in defining the ``coarse grid'' matrices

, which inherently depends on knowledge of the grid structure. This part of the preconditioner can be left out, at the expense of a deteriorating convergence rate as

increases. Radicati and Robert [178] have experimented with such an algebraic overlapping block Jacobi preconditioner.