Matrix-vector products





Next: Preconditioning
Up: Parallelism
Previous: Vector updates
The matrix-vector products are often easily parallelized on shared-memory
machines by splitting the matrix in strips corresponding to the vector
segments. Each processor then computes the matrix-vector product of one
strip.
For distributed-memory machines, there may be a problem if each processor
has only a segment of the vector in its memory. Depending on the bandwidth
of the matrix, we may need communication for other elements of the vector,
which may lead to communication bottlenecks. However, many sparse
matrix problems arise from a network in which only nearby nodes are
connected. For example, matrices stemming
from finite difference or finite element problems typically involve
only local connections: matrix element  is nonzero
only if variables
is nonzero
only if variables 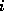 and
and 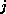 are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing
are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing 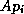 , each processor requires the values of
, each processor requires the values of 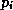 at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
For more detailed discussions on implementation aspects for distributed
memory systems, see De Sturler [63] and
Pommerell [175].
at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
For more detailed discussions on implementation aspects for distributed
memory systems, see De Sturler [63] and
Pommerell [175].
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 is nonzero
only if variables
is nonzero
only if variables 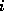 and
and 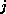 are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing
are physically close.
In such a case, it seems natural to subdivide the network, or
grid, into suitable blocks and to distribute them over the processors.
When computing 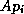 , each processor requires the values of
, each processor requires the values of 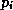 at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
For more detailed discussions on implementation aspects for distributed
memory systems, see De Sturler [63] and
Pommerell [175].
at
some nodes in neighboring blocks. If the number of connections to these
neighboring blocks is small compared to the number of internal nodes,
then the communication time can be overlapped with computational work.
For more detailed discussions on implementation aspects for distributed
memory systems, see De Sturler [63] and
Pommerell [175].