Tradeoffs



Next: Implementation and Performance
Up: Parallel Spectral Divide
Previous: Spectral Transformation Techniques
Algorithm 1 computes an explicit inverse,
which could cause numerical instability if the matrix is ill-conditioned.
The inverse free Algorithm 2 provides an alternative approach
for achieving better numerical stability. There are some
very difficult problems where Algorithm 2 gives a more
accurate answer than Algorithm 1. Numerical examples
can be found in [7]. However, neither algorithm
avoids all accuracy and convergence difficulties associated with eigenvalues very close
to the boundary of the selected region.
The stability advantage of the inverse free approach is obtained at the
cost of more storage and arithmetic.
Algorithm 2 needs 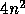 more storage space than Algorithm 1.
This will certainly limit the problem size we will be able to solve.
Furthermore, one step of the Algorithm 2 does about 6 to 7
times more arithmetic than the one step of Algorithm 1.
QR decomposition, the major component of Algorithm 2, and matrix inversion,
the main component of Algorithm 1, require comparable amounts of communication
per flop. (See table 4 for details.) Therefore,
Algorithm 2 can be expected to run significantly slower than Algorithm 1.
more storage space than Algorithm 1.
This will certainly limit the problem size we will be able to solve.
Furthermore, one step of the Algorithm 2 does about 6 to 7
times more arithmetic than the one step of Algorithm 1.
QR decomposition, the major component of Algorithm 2, and matrix inversion,
the main component of Algorithm 1, require comparable amounts of communication
per flop. (See table 4 for details.) Therefore,
Algorithm 2 can be expected to run significantly slower than Algorithm 1.
Since Algorithm 1 is faster but somewhat less stable than
Algorithm 2, and since testing stability is easy
(compute 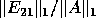 ),
we may use the following 3 step algorithm:
),
we may use the following 3 step algorithm:
- Try to use Algorithm 1 to split the spectrum. If it succeeds, stop.
- Otherwise, try to split the spectrum using Algorithm 2. If it succeeds, stop.
- Otherwise, use the QR algorithm.
This 3-step approach works by trying the fastest but least stable method first,
falling back to slower but more stable methods only if necessary. The same
paradigm is also used in other parallel algorithms [19].
If a fast parallel version of the QR algorithm[32] becomes
available, it would probably be faster than the inverse free algorithm
and hence would obviate the need for the second step listed above.
Algorithm 2 would still be of interest if only a subset of the
spectrum is desired (the QR algorithm necessarily computes the entire
spectrum), or for the generalized eigenproblem of a matrix pencil 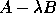 .
.



Next: Implementation and Performance
Up: Parallel Spectral Divide
Previous: Spectral Transformation Techniques
Jack Dongarra
Mon Jan 9 11:07:50 EST 1995
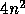 more storage space than Algorithm 1.
This will certainly limit the problem size we will be able to solve.
Furthermore, one step of the Algorithm 2 does about 6 to 7
times more arithmetic than the one step of Algorithm 1.
QR decomposition, the major component of Algorithm 2, and matrix inversion,
the main component of Algorithm 1, require comparable amounts of communication
per flop. (See table 4 for details.) Therefore,
Algorithm 2 can be expected to run significantly slower than Algorithm 1.
more storage space than Algorithm 1.
This will certainly limit the problem size we will be able to solve.
Furthermore, one step of the Algorithm 2 does about 6 to 7
times more arithmetic than the one step of Algorithm 1.
QR decomposition, the major component of Algorithm 2, and matrix inversion,
the main component of Algorithm 1, require comparable amounts of communication
per flop. (See table 4 for details.) Therefore,
Algorithm 2 can be expected to run significantly slower than Algorithm 1.
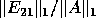 ),
we may use the following 3 step algorithm:
),
we may use the following 3 step algorithm:
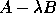 .
.