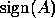 , of a matrix
, of a matrix  with
no eigenvalues on the imaginary axis can be defined via the Jordan canonical
form of
with
no eigenvalues on the imaginary axis can be defined via the Jordan canonical
form of  (2.1), where the eigenvalues of
(2.1), where the eigenvalues of  are in the
open right half plane
are in the
open right half plane 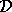 , and the eigenvalues of
, and the eigenvalues of  are in the open left
half plane
are in the open left
half plane 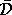 . Then
. Then 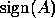 is
is
The first SDC algorithm uses the matrix sign function, which was introduced by Roberts [46] for solving the algebraic Riccati equation. However, it was soon extended to solving the spectral decomposition problem [8]. More recent studies may be found in [6][42][11].
The matrix sign function, 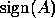 , of a matrix
, of a matrix  with
no eigenvalues on the imaginary axis can be defined via the Jordan canonical
form of
with
no eigenvalues on the imaginary axis can be defined via the Jordan canonical
form of  (2.1), where the eigenvalues of
(2.1), where the eigenvalues of  are in the
open right half plane
are in the
open right half plane 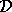 , and the eigenvalues of
, and the eigenvalues of  are in the open left
half plane
are in the open left
half plane 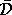 . Then
. Then 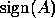 is
is

It is easy to see that the matrix
is the spectral projector onto the invariant subspace corresponding to
the eigenvalues of  in
in 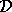 .
.
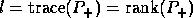 is the
number of the eigenvalues of
is the
number of the eigenvalues of  in
in 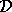 .
.
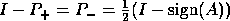 is the spectral projector
corresponding to the eigenvalues of
is the spectral projector
corresponding to the eigenvalues of  in
in 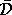 .
.
Now let 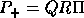 be the rank revealing QR decomposition of the
projector
be the rank revealing QR decomposition of the
projector 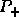 .
Then
.
Then 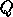 yields the desired spectral decomposition (2.3),
where the eigenvalues of
yields the desired spectral decomposition (2.3),
where the eigenvalues of 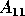 are the eigenvalues of
are the eigenvalues of  in
in 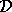 ,
and the eigenvalues of
,
and the eigenvalues of 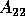 are the eigenvalues of
are the eigenvalues of  in
in 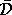 .
.
Since the matrix sign function, 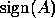 , satisfies the matrix equation
, satisfies the matrix equation
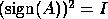 , we can use Newton's method to solve this
matrix equation and obtain the following simple iteration:
, we can use Newton's method to solve this
matrix equation and obtain the following simple iteration:
The iteration is globally and ultimately quadratically convergent with
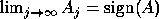 , provided
, provided  has no pure imaginary
eigenvalues [35][46].
The iteration fails otherwise,
and in finite precision, the iteration could converge slowly or not at
all if
has no pure imaginary
eigenvalues [35][46].
The iteration fails otherwise,
and in finite precision, the iteration could converge slowly or not at
all if  is ``close'' to having pure imaginary eigenvalues.
is ``close'' to having pure imaginary eigenvalues.
There are many ways to improve the accuracy and convergence rate of this
basic iteration [37][33][12].
For example, if 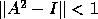 , we may use the so called
Newton-Schulz iteration
, we may use the so called
Newton-Schulz iteration
to avoid the use of the matrix inverse. Although it requires twice as many
flops, it is more efficient whenever matrix multiply is at least twice as
efficient as matrix inversion.
The Newton-Schulz iteration is also quadratically convergent provided
that 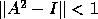 .
A hybrid iteration might begin with Newton iteration until
.
A hybrid iteration might begin with Newton iteration until
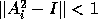 and then switch to Newton-Schulz iteration
(we discuss the performance of one such hybrid later).
and then switch to Newton-Schulz iteration
(we discuss the performance of one such hybrid later).
Hence, we have the following algorithm which divides the spectrum along the pure imaginary axis.
ALGORITHM 1 (THE SDC ALGORITHM WITH NEWTON ITERATION)
Let  ;
;
For 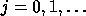 until convergence
or
until convergence
or 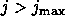 do
do
 ;
;
if 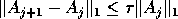 ,
,  , exit
, exit
End for;
Compute 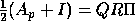 ; ~
(rank revealing QR decomposition)
; ~
(rank revealing QR decomposition)
Let 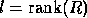 ;
;
Compute 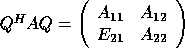 ;
;
Compute 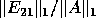 .
.
Here  is the stopping criterion for the Newton
iteration (say,
is the stopping criterion for the Newton
iteration (say, 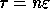 , where
, where  is the machine precision),
and
is the machine precision),
and 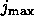 limits the
maximum number of iterations (say
limits the
maximum number of iterations (say 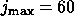 ).
On return, the generally nonzero quantity
).
On return, the generally nonzero quantity
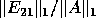 measures the backward stability of the
computed decomposition, since by setting
measures the backward stability of the
computed decomposition, since by setting 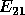 to zero and
so decoupling the problem into
to zero and
so decoupling the problem into 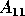 and
and 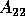 ,
a backward error of
,
a backward error of 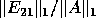 is introduced.
is introduced.
For simplicity, we just use the QR decomposition with column pivoting to reveal rank, although more sophisticated rank-revealing schemes exist [51][34][31][14].
All the variations of the Newton iteration with global convergence still need to compute the inverse of a matrix explicitly in one form or another. Dealing with ill-conditioned matrices and instability in the Newton iteration for computing the matrix sign function and the subsequent spectral decomposition is discussed in [4][6][11] and the references therein.