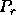 ,
, 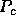 ,
,  , and
, and  , where
, where 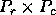 is the
process template and
is the
process template and  is the block size.
is the block size.
The way in which a matrix is distributed over the processes has a major impact on the load balance and communication characteristics of the concurrent algorithm, and hence largely determines its performance and scalability. The block cyclic distribution provides a simple, yet general-purpose way of distributing a block-partitioned matrix on distributed memory concurrent computers. It has been incorporated in the High Performance Fortran standard [11].
The block cyclic data distribution is parameterized by the four
numbers 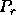 ,
, 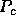 ,
,  , and
, and  , where
, where 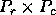 is the
process template and
is the
process template and  is the block size.
is the block size.
Suppose first that we have 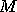 objects, indexed by an integer
objects, indexed by an integer
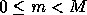 , to map onto
, to map onto 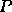 processes, using block size
processes, using block size  .
The
.
The  -th item will be stored in the
-th item will be stored in the 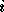 -th location of block
-th location of block 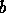 on process
on process 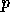 , where
, where
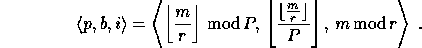
In the special case where
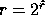 and
and 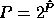 are powers of two, this mapping
is really just bit extraction, with
are powers of two, this mapping
is really just bit extraction, with 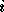 equal to the rightmost
equal to the rightmost
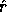 bits of
bits of  ,
, 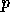 equal to the next
equal to the next  bits of
bits of  ,
and
,
and 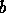 equal to the remaining leftmost bits of
equal to the remaining leftmost bits of  . The distribution
of a block-partitioned matrix can be regarded as the tensor product of
two such mappings: one that distributes the rows of the matrix over
. The distribution
of a block-partitioned matrix can be regarded as the tensor product of
two such mappings: one that distributes the rows of the matrix over
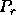 processes, and another that distributes the columns over
processes, and another that distributes the columns over 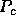 processes. That is, the matrix element indexed globally by
processes. That is, the matrix element indexed globally by 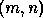 is stored in location
is stored in location
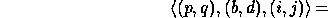
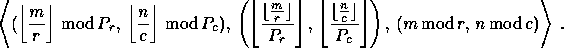
The nonscattered decomposition (or pure block distribution) is just the
special case  and
and 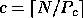 .
Similarly a purely scattered decomposition (or two dimensional wrapped
distribution) is the special case
.
Similarly a purely scattered decomposition (or two dimensional wrapped
distribution) is the special case 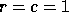 .
.