ScaLAPACK - Symmetric Eigenproblem




Next: Heterogeneous Networks
Up: Design of ScaLAPACK
Previous: ScaLAPACK - LU
The solution of the symmetric eigenproblem PDSYEVX consists
of three phases: (1) reduce the original matrix 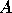 to tridiagonal
form
to tridiagonal
form 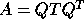 where
where  is orthogonal and
is orthogonal and 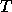 is tridiagonal, (2)
find the eigenvalues
is tridiagonal, (2)
find the eigenvalues 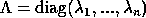 and eigenvectors
and eigenvectors 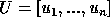 of
of 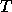 so that
so that  ,
and (3) form the eigenvector matrix
,
and (3) form the eigenvector matrix 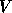 of
of 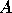 so
so
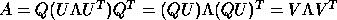 .
Phases 1 and 3 are analogous to their LAPACK counterparts,
similarly to LU. However, our current design for phase 2
differs from the serial (or shared memory) design. We have
chosen to do bisection followed by inverse iteration
(like the LAPACK expert driver DSYEVX), but with the
reorthogonalization phase of inverse iteration limited to the
eigenvectors stored in a single process. A straightforward
parallelization of DSYEVX would have led to a serial
bottleneck and significant slowdowns in the rare situation
of matrices with eigenvalues tightly clustered together.
The current design guarantees that phase (2) is inexpensive
compared to the other phases once problems are reasonably large.
An alternative algorithm which completely eliminates the need for
reorthogonalization has recently been discovered by Parlett,
Fernando, and Dhillon [17], and we expect to use this
version of the routine in the near future. This new routine
will guarantee high accuracy and high speed independent of
the eigenvalue distribution.
.
Phases 1 and 3 are analogous to their LAPACK counterparts,
similarly to LU. However, our current design for phase 2
differs from the serial (or shared memory) design. We have
chosen to do bisection followed by inverse iteration
(like the LAPACK expert driver DSYEVX), but with the
reorthogonalization phase of inverse iteration limited to the
eigenvectors stored in a single process. A straightforward
parallelization of DSYEVX would have led to a serial
bottleneck and significant slowdowns in the rare situation
of matrices with eigenvalues tightly clustered together.
The current design guarantees that phase (2) is inexpensive
compared to the other phases once problems are reasonably large.
An alternative algorithm which completely eliminates the need for
reorthogonalization has recently been discovered by Parlett,
Fernando, and Dhillon [17], and we expect to use this
version of the routine in the near future. This new routine
will guarantee high accuracy and high speed independent of
the eigenvalue distribution.
Antoine Petitet
Fri Mar 31 13:01:26 EST 1995
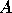 to tridiagonal
form
to tridiagonal
form 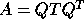 where
where  is orthogonal and
is orthogonal and 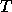 is tridiagonal, (2)
find the eigenvalues
is tridiagonal, (2)
find the eigenvalues 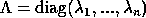 and eigenvectors
and eigenvectors 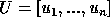 of
of 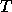 so that
so that  ,
and (3) form the eigenvector matrix
,
and (3) form the eigenvector matrix 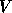 of
of 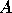 so
so
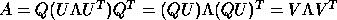 .
Phases 1 and 3 are analogous to their LAPACK counterparts,
similarly to LU. However, our current design for phase 2
differs from the serial (or shared memory) design. We have
chosen to do bisection followed by inverse iteration
(like the LAPACK expert driver DSYEVX), but with the
reorthogonalization phase of inverse iteration limited to the
eigenvectors stored in a single process. A straightforward
parallelization of DSYEVX would have led to a serial
bottleneck and significant slowdowns in the rare situation
of matrices with eigenvalues tightly clustered together.
The current design guarantees that phase (2) is inexpensive
compared to the other phases once problems are reasonably large.
An alternative algorithm which completely eliminates the need for
reorthogonalization has recently been discovered by Parlett,
Fernando, and Dhillon [17], and we expect to use this
version of the routine in the near future. This new routine
will guarantee high accuracy and high speed independent of
the eigenvalue distribution.
.
Phases 1 and 3 are analogous to their LAPACK counterparts,
similarly to LU. However, our current design for phase 2
differs from the serial (or shared memory) design. We have
chosen to do bisection followed by inverse iteration
(like the LAPACK expert driver DSYEVX), but with the
reorthogonalization phase of inverse iteration limited to the
eigenvectors stored in a single process. A straightforward
parallelization of DSYEVX would have led to a serial
bottleneck and significant slowdowns in the rare situation
of matrices with eigenvalues tightly clustered together.
The current design guarantees that phase (2) is inexpensive
compared to the other phases once problems are reasonably large.
An alternative algorithm which completely eliminates the need for
reorthogonalization has recently been discovered by Parlett,
Fernando, and Dhillon [17], and we expect to use this
version of the routine in the near future. This new routine
will guarantee high accuracy and high speed independent of
the eigenvalue distribution.