 Available Operations
Available Operations
 Available Operations
Available OperationsThe choice between different methods very much depends on which of these operations one has available at a reasonable cost. We list the major ones in decreasing order of power:
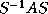 can be applied to
matrices
can be applied to
matrices  of reasonable size, stored as two dimensional arrays,
or in a dense band structure. (For pencils
of reasonable size, stored as two dimensional arrays,
or in a dense band structure. (For pencils  , we
would use equivalence transformations
, we
would use equivalence transformations
 instead).
Many of these algorithms have good implementations available
[1]. Some of them (such as sign function
based algorithms [5]) are currently being implemented.
When good ``black-box'' implementations exist, they will not be described
in detailed templates. We will however indicate when they are to be
preferred over the iterative methods, which are the main
theme of this collection.
instead).
Many of these algorithms have good implementations available
[1]. Some of them (such as sign function
based algorithms [5]) are currently being implemented.
When good ``black-box'' implementations exist, they will not be described
in detailed templates. We will however indicate when they are to be
preferred over the iterative methods, which are the main
theme of this collection.
 by a shifted-and-inverted
operator,
by a shifted-and-inverted
operator,  or
or 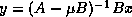 for a given vector
for a given vector  , lets us quickly compute the eigenvalues
closest to the shift
, lets us quickly compute the eigenvalues
closest to the shift 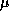 . This operation may be implemented
with an explicit triangular factorization
. This operation may be implemented
with an explicit triangular factorization
e.g. as a part of an FEM (finite element method) package,
but any other implementation may also be used, such
as those based on multigrid or more specialized methods.
It is also possible to use an iterative solver which only uses
multiplication by  (or
(or  and
and 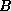 ) internally, but this
may not be superior to other methods discussed below.
) internally, but this
may not be superior to other methods discussed below.
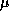 is restricted, say to 0, then
we will be restricted to efficiently finding eigenvalues
closest to zero, and will need more iterations
to find any but the few smallest eigenvalues.
is restricted, say to 0, then
we will be restricted to efficiently finding eigenvalues
closest to zero, and will need more iterations
to find any but the few smallest eigenvalues.
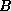 is factorizable,
e.g. if
is factorizable,
e.g. if  , so that we can only multiply vectors by
, so that we can only multiply vectors by 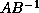 ,
we will be restricted to efficiently finding the peripheral
eigenvalues, i.e. those eigenvalues near the ``edges'' of the spectrum,
when the spectrum is seen as a set in the complex plane.
,
we will be restricted to efficiently finding the peripheral
eigenvalues, i.e. those eigenvalues near the ``edges'' of the spectrum,
when the spectrum is seen as a set in the complex plane.
If, in a special purpose method, it is possible to multiply a vector by
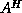 in addition to
in addition to  , or possibly
, or possibly 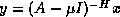 or
or
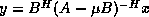 , depending on the situation, then a broader,
more powerful class of algorithms are available.
, depending on the situation, then a broader,
more powerful class of algorithms are available.
Sometimes it is significantly cheaper to apply the operator to a set of vectors rather than just 1 vector at a time. This can happen because of memory hierarchy effects. There are algorithms to exploit this behavior.
The worst case is when the only operation we can perform is multiplication
of a vector by  (and possibly
(and possibly 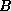 ). But algorithms are available in this
case too.
). But algorithms are available in this
case too.
Not only the matrix-vector operations but also the vector algebra needs
special consideration. In all the algorithms that we will consider,
only two different vector operations have to be applied to vectors
of length  , dot products and the addition of a multiple of one vector
to another, axpy to use terminology from the BLAS.
These operations may be implemented on distributed processors in a way
that is appropriate for the application or the computer at hand.
In some cases a vector is not even represented as an array of numbers,
but stands for a function represented in e.g. a finite element or
wavelet basis. Then user-supplied routines for dot products and axpy
will replace the basic vector operations in our templates.
, dot products and the addition of a multiple of one vector
to another, axpy to use terminology from the BLAS.
These operations may be implemented on distributed processors in a way
that is appropriate for the application or the computer at hand.
In some cases a vector is not even represented as an array of numbers,
but stands for a function represented in e.g. a finite element or
wavelet basis. Then user-supplied routines for dot products and axpy
will replace the basic vector operations in our templates.