First, we define the type of partition of 
that we are considering.
Let an integer vector 
and an integer block size parameter 
be given.
The partition induced by 
and is given by (1) where
(Imagine a knife aligned so that is normal to its flat side, cutting into slices of equal
thickness .)
We associate with and D the dependence graph 
with vertices and edges
We assume that G is acyclic. (If the dependence graph comes from a loop nest in an imperative
language like Fortran, then G has to be acyclic.)
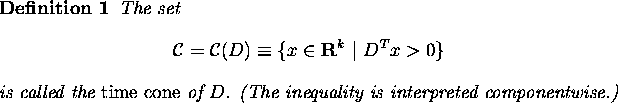
Note that 
is an open, convex set closed under multiplication by a positive scalar - i.e., is in fact a
cone. It is polygonal, the intersection of the half spaces 
.
We call the time cone, without mentioning D, whenever there is no ambiguity.
The closure of is also important; it is defined by
Two subsets of 
are important here. First, we must choose, as the normals
to the hyperplanes used to partition , integer vectors in . The intersection of with the
surface of the unit sphere in 
(with the euclidean norm) also plays a role.
For the proof, observe that the iterations may be performed in order of increasing value of 
where
x is any vector in . Because all dependence displacements 
make an acute angle with such an x,
no dependence constraint is violated.
We may therefore interpret as the time at which iteration i is to be performed, hence the name we have
given . Points of with equal value of are independent of one
another and can be executed in any order - or in parallel, for that matter. This is the essence of
Lamport's hyperplane method for the parallel execution of do-loops [13].
Again, if D results from a loop nest in Fortran or a language like it, we can show that is not empty.
In fact, it is easy to see that D has the property that the first nonzero element of every column is positive
(i.e. it is lexicographically positive.)
From this, the nonemptyness of easily follows.
We can now show how to choose hyperplanes for partitioning in such a manner that Wolfe's
atomicity requirement is satisfied. First, we restate the requirement in terms of the quotient of the
dependence graph under the partition (1).
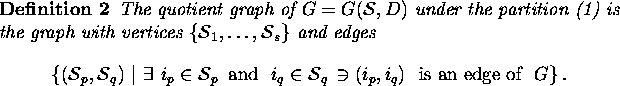
The atomicity requirement is equivalent to the requirement that the quotient graph be acyclic. A sufficient condition for this is the following.
For the proof, observe that, by their definition,
the subsets of the partition induced by and may be ordered
according to the values taken by 
on them. It follows from the definition of
that no point in a lower numbered subset can depend on any point in a higher numbered subset;
if there were such a pair, say a point x that depends on a point y such that x - y = d for
some column d of D, then d makes an obtuse angle with , i.e., 
,
since by assumption 
. But by definition, 
for all columns d of D.
Moldovan and Fortes [15] have used this technique for the synthesis of systolic arrays without cyclic data flow, which allows the array to be used to solve problems larger than the array. They gave no method for choosing the hyperplanes. The material of this section was also presented by Irigoin and Triolet [11].