Strip Mining and Loop Interchange Are Not Enough

Consider the one-dimensional, discrete diffusion process

 mmmmmmmmmm¯

for t = 0 to m do

		for i = 1 to n-1 do  

				; od

		od  

At each time step (each iteration of the t loop) at every grid point, the value of u(i) is updated by using the data at the three grid points i-1, i, and i+1 from the previous time step, t-1. This process is typical of PDE computations. Let us apply strip mining and loop interchange to this code. The resulting program, which follows, is incorrect.

 mmmmmmmmmm¯

for t0 = 0 to m step bt do

		for i0 = 1 to n-1 step bi do  

				for t = t0 to  do

						for i = i0 to  do  

								; od

						od  

				od  

		od  

One cannot advance the computation in time for a fixed subset of the grid points without advancing it for their neighbors; to update the values at the edge of the block of grid points, we require values from neighboring grid points outside the block that have not been computed. In other words, the loop interchanges that we performed were illegal and, the transformed program produces meaningless results.

Wolfe's second paper on tiling recognizes this fact. He advocates the use of a technique called loop skewing [19]. (This was also discussed by Irigoin and Triolet [11].) By loop skewing, Wolfe means changing the index of the inner loop from the natural variable (i above) to the sum or difference of the old inner index and an integer multiple of the outer loop index. With this transformation, the code above can be changed as follows:

 mmmmmmmmmm¯

for t = 0 to m do

		for r = t+1 to t+n-1 do  

				; od

		od  

Here we have used r = i + t as the inner loop index. Note that the inner loop now ranges over oblique lines in the (i,t) plane. We may now legally strip mine and interchange to get a tiled program:

 mmmmmmmmmmmmm¯

for t0 = 0 to m step bt do

		for r0 = t0 + 1 to t0+n-1 step br do  

				for t = t0 to  do

						for  to  do  

								u[r-t,t] =

										f(u[r-t-1,t-1], u[r-t,t-1], u[r-t+1,t-1]); od

						od  

				od  

		od  

Figure 1 shows the tiles of computation in the original coordinates (i,t).

  
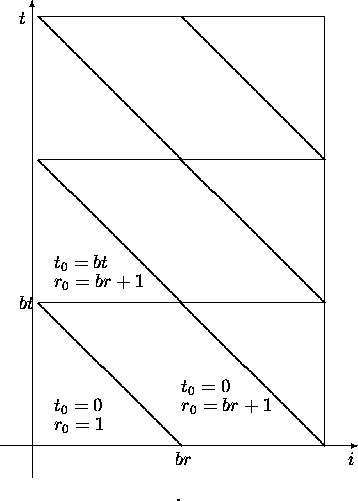
Figure 1: Tiled index space, with new inner index .

In this paper, we consider the following generalization of Wolfe's loop skewing. We allow all of the loop indices to be replaced by linear combinations of the original, natural indices. Let the computation be a loop nest of depth k. Let the natural indices be . Let A be an invertible, integer matrix. We would like to use as the indices in a transformed program, where

We can carry out this transformation in two steps. First, we replace every reference to any of the natural loop indices in the program by a reference to the equivalent linear combination of the transformed indices. If the rational matrix ( denotes the inverse of ), then we replace a reference to , for example, by the linear combination

Second, we compute upper and lower bounds on the transformed indices. We call this program rewriting technique loop index transformation.

The first contribution of this work is a method for choosing the loop index transformation A. We start from the assumption that the computation is a nested loop of depth k in which there are some loop-carried dependences with fixed displacements in the index space. We then consider the problem of determining which loop index transformations A permit the resulting index-transformed loop nest to be successfully tiled through strip mining and interchange. (The mechanics of automating these program transformation is discussed in the compiler optimization literature [3].) We show that this problem amounts to a purely geometric one: finding a basis for real k-space consisting of vectors with integer components that are constrained to lie in a certain closed, polygonal cone defined by the dependence displacements. The basis vectors are then taken to be the columns of the loop index transformation A. We further show that the amount of reuse that can be achieved with a given amount of local memory, which is determined by the ratio of the number of iterations in a tile to the amount of data required by the tile, is dependent on A in a simple way. It is proportional to the root of where is the matrix obtained by scaling the columns of A to have euclidean length one.

We give a heuristic procedure for determining such an integer matrix A that approximately maximizes this determinant. We report on the results of some experiments to test its performance and robustness.

Finally, we consider the optimal choice of tile size and shape, once the basis A has been determined. We show that it is straightforward to derive block size parameters that maximize the ratio of computation in a tile to data required by the tile, given knowledge of the flux of data in the index space and the blocking basis A.