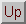
Figure 5: 1-, 2-, 3-, and 4-dimensional hypercube connections.



The class of DM-MIMD machines is undoubtly the fastest growing part in the family of high-performance computers. Although this type of machines is more difficult to deal with than shared-memory machines and DM-SIMD machines. The latter type of machines are processor-array systems in which the data structures that are candidates for parallelisation are vectors and multi-dimensional arrays that are laid out automatically on the processor array by the system software. For shared-memory systems the data distribution is completely transparant to the user. This is quite different for DM-MIMD systems where the user has to distribute the data over the processors and also the data exchange between processors has to be performed explicitely. The initial reluctance to use DM-MIMD machines seems to have been decreased. Partly this is due to the now existing standard for communication software ([8,15]) and partly because, at least theoretically, this class of systems is able to outperform all other types of machines.
The advantages of DM-MIMD systems are clear: the bandwidth problem that haunts shared-memory systems is avoided because the bandwidth scales up automatically with the number of processors. Furthermore, the speed of the memory which is another critical issue with shared-memory systems (to get a peak performance that is comparable to that of DM-MIMD systems, the processors of the shared-memory machines should be very fast and the speed of the memory should match it) is less important for the DM-MIMD machines, because more processors can be configured without the afore mentioned bandwidth problems.
Of course, DM-MIMD systems also have their disadvantages: The communication between processors is much slower than in SM-MIMD systems, and so, the synchronisation overhead in case of communicating tasks is generally orders of magnitude higher than in shared-memory machines. Moreover, the access to data that are not in the local memory belonging to a particular processor have to be obtained from non-local memory (or memories). This is again on most systems very slow as compared to local data access. When the structure of a problem dictates a frequent exchange of data between processors and/or requires many processor synchronisations, it may well be that only a very small fraction of the theoretical peak speed can be obtained. As already mentioned, the data- and task decomposition are factors that mostly have to be dealt with explicitly, which may be far from trivial.
It will be clear from the paragraph above that also for DM-MIMD machines both the topology and the speed of the datapaths are of crucial importance for the practical usefulness of a system. Again, as in the section on SM-MIMD systems, the richness of the connection structure has to be balanced against the costs. Of the many conceivable interconnection structures only a few are popular in practice. One of these is the so-called hypercube topology as depicted in Figure 5.

Figure 5: 1-, 2-, 3-, and 4-dimensional hypercube connections.
A nice feature of the hypercube topology is that for a hypercube with 2d nodes the number of steps to be taken between any two nodes is at most d. So, the dimension of the network grows only logarithmically with the number of nodes. In addition, theoretically, it is possible to simulate any other topology on a hypercube: trees, rings, 2-D and 3-D meshes, etc. In practice, the exact topology for hypercubes do not matter too much anymore because all systems in the market today employ what is called "wormhole routing". This means that a message is send from one node to another node that it wants to communicate with to set up a direct connection between them. As soon this connection is established, the data proper is sent through this connection without disturbing the operation of the intermediate nodes. Except for a small amount of time in setting up the connection between nodes, the communication time has become virtually independent of the distance between the nodes. Of course, when several messages in a busy network have to compete for the same paths, waiting times are incurred as in any network that does not directly connect any processor to all others and often rerouting strategies are employed to circumvent busy links.
Many of the newly introduced massively parallel DM-MIMD systems seem to favour a 2- or 3-D mesh (torus) structure. The rationale for this seems to be that most large-scale physical simulations can be mapped efficiently on this topology and that a richer interconnection structure hardly pays off. However, some systems maintain (an) additional network(s) besides the mesh to handle certain bottlenecks in data distribution and retrieval [10].
A large fraction of systems in the DM-MIMD class employ crossbars. For
relatively small amounts of processors (in the order of 64) this may be
a direct or 1-stage crossbar, while to connect larger numbers of nodes
multi-stage crossbars are used, i.e., the connections of a crossbar at
level 1 connect to a crossbar at level 2, etc., instead of directly to
nodes at more remote distances in the topology. In this way it is
possible to connect in the order of a few thousands of nodes through
only a few switching stages. Butterfly-, ![]() -, or shuffle-exchange
networks are often employed in such systems.
-, or shuffle-exchange
networks are often employed in such systems.
As with SM-MIMD machines, a node may in principle consist of any type of processor (scalar or vector) for computation or transaction processing together with local memory (with or without cache) and, in almost all cases, a separate communication processor with links to connect the node to its neighbours. Nowadays, the node processors are mostly off-the-shelf RISC processors sometimes enhanced by vector processors. A problem that is peculiar to this DM_MIMD systems is the mismatch of communication vs. computation speed that may occur when the node processors are upgraded, without also speeding up the intercommunication. In some cases this may result in turning computational-bound problems into communication-bound problems.