Tests for the ScaLAPACK SVD routines

The following tests will be performed on PSGESVD/PDGESVD. A number of matrix ``types'' are specified, as denoted in Table 2. For each type of matrix, and for the minimal workspace as well as for larger than minimal workspace an $M$-by$N$ matrix ``A'' with known singular values is generated and used to test the SVD routines. For each matrix, A will be factored as $A~=~U~diag(S)~VT$ and the following 9 tests computed:

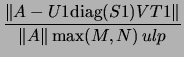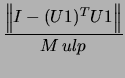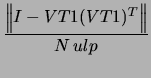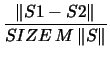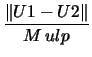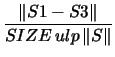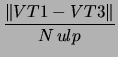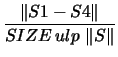$$r_1 = \frac{ \left\Vert A - U1 \mbox{diag}(S1) VT1 \right\Vert} { \left\Vert A\right\Vert\max(M,N) \, ulp}$$

$$r_2 = \frac{ \left\Vert I - (U1)^T U1 \right\Vert} { M \, ulp}$$

$$r_3 = \frac{ \left\Vert I - VT1 (VT1)^T \right\Vert} { N \, ulp}$$

$$r_4 = \left\{ \begin{array}{ll} 0 & \mbox{if $S1$\ contains SIZE nonneg... ...s in decreasing order.} \\ \frac{1}{ulp} & \mbox{otherwise} \end{array}\right.$$

$$r_5 = \frac{ \left\Vert S1 - S2 \right\Vert} { SIZE \, M \left\Vert S\right\Vert}$$

$$r_6 = \frac{ \left\Vert U1 - U2 \right\Vert} { M \, ulp}$$

$$r_7 = \frac{ \left\Vert S1 - S3 \right\Vert} { SIZE \, ulp \left\Vert S\right\Vert}$$

$$r_8 = \frac{ \left\Vert VT1 - VT3 \right\Vert} { N \, ulp}$$

$$r_9 = \frac{ \left\Vert S1 - S4 \right\Vert} { SIZE \, ulp \, \left\Vert S\right\Vert}$$

where $ulp$ represents PxLAMCH(ICTXT, 'P').