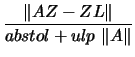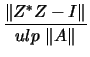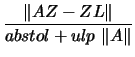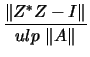Next: Test Matrices for the
Up: More About the ScaLAPACK
Previous: Input File for Testing
Contents
The following tests will be performed on PxSYEV/PxHEEV, PxSYEVX/PxHEEVX and
PxSYEVD/PxHEEVD:
where 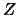 is the matrix of eigenvectors returned when the
eigenvector option is given,
is the matrix of eigenvectors returned when the
eigenvector option is given, 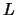 is the matrix of eigenvalues,
is the matrix of eigenvalues,
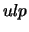 represents PxLAMCH( ICTXT, 'P' ),
and
represents PxLAMCH( ICTXT, 'P' ),
and 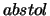 represents
represents
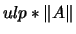 .
.
The tester allows multiple test requests to be controlled from a
single input file. Each test request is controlled by the following inputs:
- Values of N
N = The matrix size
- Values of P, Q, NB
P = NPROW, the number of processor rows
Q = NPCOL, the number of processor columns
NB = the block size
- Values of the matrix types
See Section 3.11.1.
- Number of eigen requests
1 = Test full eigendecomposition only
8 = Test the following eigen requests:
Full eigendecomposition
All eigenvalues, no eigenvectors
Eigenvalues requested by value (i.e. VL,VU)
Eigenvalues and vectors requested by value
Eigenvalues requested by index (i.e. IL, IU)
Eigenvalues and vectors requested by index
Full eigendecomposition with minimal workspace provided
Full eigendecomposition with random workspace provided
- Threshold
The highest value of 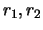 and
and 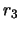 that will be accepted.
that will be accepted.
- Absolute tolerance
Must be -1.0 to ensure orthogonal eigenvectors
- Print Request
1 = Print every test
2 = Print only failing tests and a summary of the request
Subsections




Next: Test Matrices for the
Up: More About the ScaLAPACK
Previous: Input File for Testing
Contents
Susan Blackford
2001-08-12