| I |
RP(I) |
u |
definition |
| 1 |
RLTRGT |
u |
target value for 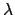
|
| 2 |
RTRGT |
u |
target value for
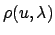
|
| 3 |
RMTRGT |
u |
target value for 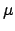
|
| 4 |
RLLWR |
u |
lower bound for 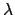
|
| 5 |
RLUPR |
u |
upper bound for 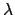
|
| 6 |
DTOL |
u |
drop tolerance for incomplete factorization |
| 8 |
SMIN |
u |
lower limit for contour colors |
| 9 |
SMAX |
u |
upper limit for contour colors |
| 10 |
RMAG |
u |
window magnification factor |
| 11 |
CENX |
u |
(CENX,CENY) are the window center coordinates |
| 12 |
CENY |
u |
|
| 15 |
HMAX |
u |
approximate largest element size |
| 16 |
GRADE |
u |
largest growth factor for adjacent elements |
| 17 |
HMIN |
u |
approximate smallest edge length |
| 21 |
RL |
|
current value of 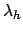
|
| 22 |
R |
|
current value of
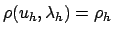
|
| 23 |
RLDOT |
|
current value of
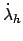
|
| 24 |
RDOT |
|
current value of
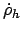
|
| 25 |
SVAL |
|
current value of smallest singular value |
| 26 |
RLSTRT |
|
starting value for 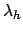
|
| 27 |
RSTRT |
|
starting value for
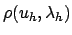
|
| 31 |
RL0 |
|
previous value of 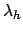
|
| 32 |
R0 |
|
previous value of
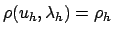
|
| 33 |
RL0DOT |
|
previous value of
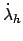
|
| 34 |
R0DOT |
|
previous value of
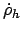
|
| 35 |
SVAL0 |
|
previous value of smallest singular value |
| 37 |
ENORM1 |
|
estimate for
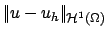
|
| 38 |
UNORM1 |
|
the norm
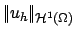
|
| 39 |
ENORM2 |
|
estimate for
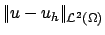
|
| 40 |
UNORM2 |
|
the norm
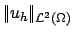
|
| 51 |
EPS |
|
the machine epsilon |
| 52 |
STEP |
|
damping step 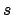 for Newton's method
for Newton's method |
| 53 |
RELER0 |
|
relative size of solution error
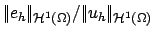
|
| 54 |
RELERR |
|
relative size of Newton update
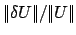
|
| 55 |
ANORM |
|
maximum diagonal entry in Jacobian matrix |
| 56 |
RELRES |
|
the relative residual
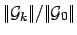
|
| 57 |
BRATIO |
|
the relative residual
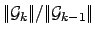
|
| 58 |
DNEW |
|
the discrete inner product
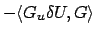
|
| 59 |
BNORM0 |
|
scaling factor
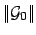
|
| 60 |
BMNRM0 |
|
scaling factor for 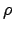
|
| 63 |
RMU |
|
current value of 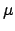
|
| 64 |
REG |
|
internal regularization parameter |
| 67 |
SCLEQN |
|
current value of scalar equation 
|
| 68 |
SCALE |
|
scaling factor for scalar equation |
| 69 |
THETAL |
|
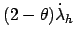 in scalar equation
in scalar equation |
| 70 |
THETAR |
|
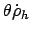 in scalar equation
in scalar equation |
| 71 |
SIGMA |
|
the step 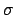 for scalar equation
for scalar equation |
| 72 |
DELTA |
|
Newton update for 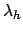
|
| 73 |
DRDRL |
|
the value of
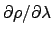
|
| 74 |
SEQDOT |
|
the value of 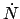
|
| 76 |
QUAL |
|
target element quality |
| 77 |
ANGMN |
|
target minimum angle |
| 78 |
DIAM |
|
approximate diameter of 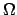
|
| 79 |
BEST |
|
value of TRIGEN quality function |
| 80 |
AREA |
|
area of 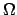
|
| 81 |
TOLA |
|
angle tolerance |
| 82 |
ARCMIN |
|
minimum arc |
| 83 |
ARCMAX |
|
maximum arc |
| 84 |
TOLZ |
|
contour tolerance |
| 85 |
TOLF |
|
function value tolerance |
| 87 |
XMIN |
|
|
| 88 |
XMAX |
|
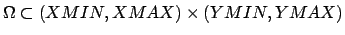
|
| 89 |
YMIN |
|
|
| 90 |
YMAX |
|
|