Sparse Incomplete Factorizations





Next: Generating a CRS-based
Up: Data Structures
Previous: CDS Matrix-Vector Product
Efficient preconditioners for iterative methods can be found by
performing an incomplete factorization of the coefficient matrix. In
this section, we discuss the incomplete factorization of an 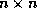 matrix
matrix 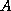 stored in the CRS format,
and routines to solve a system with such a factorization. At first we
only consider a factorization of the
stored in the CRS format,
and routines to solve a system with such a factorization. At first we
only consider a factorization of the 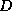 -
-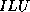 type, that is,
the simplest type of factorization in which no ``fill'' is
allowed, even if the matrix has a nonzero in the fill position (see
section
type, that is,
the simplest type of factorization in which no ``fill'' is
allowed, even if the matrix has a nonzero in the fill position (see
section  ). Later we will consider factorizations that
allow higher levels of fill. Such factorizations considerably more
complicated to code, but they are essential for complicated
differential equations. The solution routines are applicable in
both cases.
). Later we will consider factorizations that
allow higher levels of fill. Such factorizations considerably more
complicated to code, but they are essential for complicated
differential equations. The solution routines are applicable in
both cases.
For iterative methods, such as 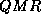 , that involve a transpose matrix
vector product we need to consider solving a system with the transpose
of as factorization as well.
, that involve a transpose matrix
vector product we need to consider solving a system with the transpose
of as factorization as well.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
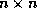 matrix
matrix 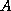 stored in the CRS format,
and routines to solve a system with such a factorization. At first we
only consider a factorization of the
stored in the CRS format,
and routines to solve a system with such a factorization. At first we
only consider a factorization of the 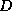 -
-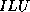 type, that is,
the simplest type of factorization in which no ``fill'' is
allowed, even if the matrix has a nonzero in the fill position (see
section
type, that is,
the simplest type of factorization in which no ``fill'' is
allowed, even if the matrix has a nonzero in the fill position (see
section 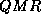 , that involve a transpose matrix
vector product we need to consider solving a system with the transpose
of as factorization as well.
, that involve a transpose matrix
vector product we need to consider solving a system with the transpose
of as factorization as well.
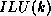 Incomplete Factorization
Incomplete Factorization