More Details about Stopping Criteria





Next: When or is
Up: Stopping Criteria
Previous: Stopping Criteria
Ideally we would like to stop when the magnitudes of entries of the error
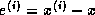 fall below a user-supplied threshold.
But
fall below a user-supplied threshold.
But 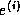 is hard to estimate directly, so
we use the residual
is hard to estimate directly, so
we use the residual 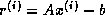 instead, which is
more readily computed. The rest of this section describes how to measure
the sizes of vectors
instead, which is
more readily computed. The rest of this section describes how to measure
the sizes of vectors 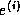 and
and  , and how to bound
, and how to bound 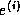 in terms of
in terms of  .
.
We will measure errors using vector and matrix norms.
The most common vector norms are:

For some algorithms we may also use the norm
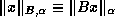 , where
, where 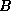 is a fixed nonsingular
matrix and
is a fixed nonsingular
matrix and  is one of
is one of 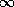 ,
,  , or
, or 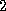 .
Corresponding to these vector norms are three matrix norms:
.
Corresponding to these vector norms are three matrix norms:
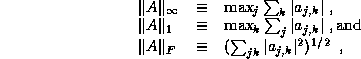
as well as  .
We may also use the matrix norm
.
We may also use the matrix norm
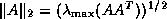 , where
, where  denotes the largest eigenvalue.
Henceforth
denotes the largest eigenvalue.
Henceforth  and
and 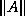 will refer to any mutually
consistent pair of the above.
(
will refer to any mutually
consistent pair of the above.
(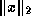 and
and  , as well as
, as well as 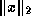 and
and 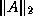 , both form
mutually consistent pairs.)
All these norms satisfy the triangle inequality
, both form
mutually consistent pairs.)
All these norms satisfy the triangle inequality  and
and 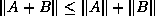 , as well as
, as well as  for mutually consistent pairs.
(For more details on the properties of norms, see Golub and
Van Loan [109].)
for mutually consistent pairs.
(For more details on the properties of norms, see Golub and
Van Loan [109].)
One difference between these norms is their dependence on dimension.
A vector  of length
of length  with entries uniformly distributed between
0 and 1 will satisfy
with entries uniformly distributed between
0 and 1 will satisfy 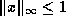 , but
, but 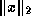 will grow
like
will grow
like  and
and 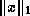 will grow like
will grow like  . Therefore a stopping
criterion based on
. Therefore a stopping
criterion based on 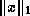 (or
(or 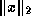 ) may have to be permitted to
grow proportional to
) may have to be permitted to
grow proportional to  (or
(or  ) in order that it does not become
much harder to satisfy for large
) in order that it does not become
much harder to satisfy for large  .
.
There are two approaches to bounding the
inaccuracy of the computed solution to  .
Since
.
Since  ,
which we will call the forward error,
is hard to estimate directly,
we introduce
the backward error, which allows us to bound the forward error.
The normwise backward error is defined as
the smallest possible value of
,
which we will call the forward error,
is hard to estimate directly,
we introduce
the backward error, which allows us to bound the forward error.
The normwise backward error is defined as
the smallest possible value of
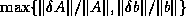 where
where
 is the exact solution of
is the exact solution of 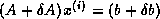 (here
(here 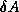 denotes a general matrix, not
denotes a general matrix, not  times
times  ; the
same goes for
; the
same goes for  ).
The backward error may be easily computed from the residual
).
The backward error may be easily computed from the residual
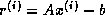 ; we show how below.
Provided one has
some bound on the inverse of
; we show how below.
Provided one has
some bound on the inverse of  ,
one can bound the forward error in terms of the backward error via
the simple equality
,
one can bound the forward error in terms of the backward error via
the simple equality
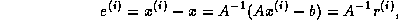
which implies 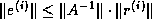 .
Therefore, a stopping criterion of the form ``stop when
.
Therefore, a stopping criterion of the form ``stop when  '' also yields an upper bound on the forward error
'' also yields an upper bound on the forward error
 . (Sometimes we may prefer to
use the stricter but harder to estimate bound
. (Sometimes we may prefer to
use the stricter but harder to estimate bound 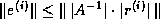 ; see §
; see § . Here
. Here
 is the matrix or vector of absolute values of components of
is the matrix or vector of absolute values of components of
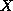 .)
.)
The backward error also has a direct interpretation as a stopping
criterion, in addition to supplying a bound on the forward error.
Recall that the backward error is the smallest change
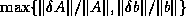 to the problem
to the problem  that makes
that makes  an exact solution of
an exact solution of
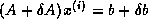 . If the original data
. If the original data  and
and 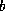 have
errors from previous computations or measurements,
then it is usually not worth iterating until
have
errors from previous computations or measurements,
then it is usually not worth iterating until 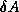 and
and  are even
smaller than these errors.
For example, if the machine precision is
are even
smaller than these errors.
For example, if the machine precision is  , it is not
worth making
, it is not
worth making  and
and
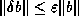 , because just rounding the entries
of
, because just rounding the entries
of  and
and 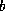 to fit in the machine creates errors this large.
to fit in the machine creates errors this large.
Based on this discussion, we will now consider
some stopping criteria and their
properties. Above we already mentioned
- Criterion 1.
-
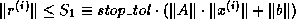 .
This is equivalent to asking that
the backward error
.
This is equivalent to asking that
the backward error 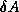 and
and  described above satisfy
described above satisfy
 and
and
 .
This criterion yields the forward error bound
.
This criterion yields the forward error bound

The second stopping criterion we discussed, which does not require 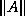 ,
may be much more stringent than Criterion 1:
,
may be much more stringent than Criterion 1:
- Criterion 2.
-
 .
This is equivalent to asking that
the backward error
.
This is equivalent to asking that
the backward error 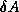 and
and  satisfy
satisfy
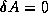 and
and 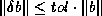 .
One difficulty with this method is that if
.
One difficulty with this method is that if 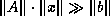 ,
which can only occur if
,
which can only occur if  is very ill-conditioned and
is very ill-conditioned and  nearly
lies in the null space of
nearly
lies in the null space of  ,
then it may be difficult
for any method to satisfy the stopping criterion. To see that
,
then it may be difficult
for any method to satisfy the stopping criterion. To see that  must
be very ill-conditioned, note that
must
be very ill-conditioned, note that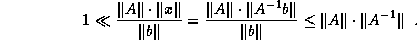
This criterion yields the forward error bound

If an estimate of  is available, one can also just stop
when the upper bound on the error
is available, one can also just stop
when the upper bound on the error  falls below
a threshold. This yields the third stopping criterion:
falls below
a threshold. This yields the third stopping criterion:
- Criterion 3.
-
 .
This stopping criterion guarantees that
.
This stopping criterion guarantees that
permitting the user to specify the desired relative accuracy stop_tol
in the computed solution  .
.
One drawback to Criteria 1 and 2 is that they usually treat backward errors in
each component of 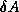 and
and  equally, since most
norms
equally, since most
norms  and
and  measure each entry of
measure each entry of 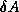 and
and  equally.
For example, if
equally.
For example, if  is sparse and
is sparse and 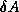 is dense, this loss of
possibly important structure will not be reflected in
is dense, this loss of
possibly important structure will not be reflected in  .
In contrast, the following stopping criterion gives one the option of scaling
each component
.
In contrast, the following stopping criterion gives one the option of scaling
each component 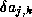 and
and 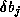 differently,
including the possibility of insisting that some entries be zero.
The cost is an extra matrix-vector multiply:
differently,
including the possibility of insisting that some entries be zero.
The cost is an extra matrix-vector multiply:
- Criterion 4.
-
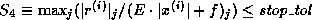 .
Here
.
Here  is a user-defined matrix of nonnegative entries,
is a user-defined matrix of nonnegative entries,
 is a user-defined vector of nonnegative entries, and
is a user-defined vector of nonnegative entries, and
 denotes the vector of absolute values of the entries of
denotes the vector of absolute values of the entries of  .
If this criterion is satisfied, it means there are a
.
If this criterion is satisfied, it means there are a 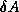 and a
and a  such that
such that
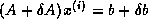 , with
, with
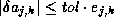 , and
, and
 for all
for all 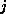 and
and  .
By choosing
.
By choosing  and
and  , the user can vary the way
the backward error is measured
in the stopping criterion. For example, choosing
, the user can vary the way
the backward error is measured
in the stopping criterion. For example, choosing 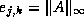 and
and 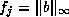 makes the stopping criterion
makes the stopping criterion
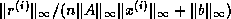 ,
which is essentially the same as Criterion 1. Choosing
,
which is essentially the same as Criterion 1. Choosing  and
and
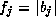 makes the stopping criterion measure the
componentwise relative backward error, i.e., the smallest relative
perturbations in any component of
makes the stopping criterion measure the
componentwise relative backward error, i.e., the smallest relative
perturbations in any component of  and
and 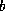 which is necessary to make
which is necessary to make
 an exact solution. This tighter stopping criterion requires, among other
things, that
an exact solution. This tighter stopping criterion requires, among other
things, that 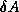 have the same sparsity pattern as
have the same sparsity pattern as  .
Other choices of
.
Other choices of  and
and  can be used to reflect other structured
uncertainties in
can be used to reflect other structured
uncertainties in  and
and 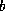 .
This criterion yields the forward error bound
.
This criterion yields the forward error bound
where  is the matrix of absolute values of entries of
is the matrix of absolute values of entries of  .
.
Finally, we mention one more criterion, not because we recommend it,
but because it is widely used. We mention it in order to explain its
potential drawbacks:
- Dubious Criterion 5.
-
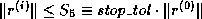 .
This commonly used criterion has the disadvantage of depending too strongly
on the initial solution
.
This commonly used criterion has the disadvantage of depending too strongly
on the initial solution 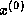 . If
. If  , a common choice, then
, a common choice, then
 . Then this criterion is equivalent to Criterion 2 above, which
may be difficult to satisfy for any algorithm
if
. Then this criterion is equivalent to Criterion 2 above, which
may be difficult to satisfy for any algorithm
if  .
On the other hand, if
.
On the other hand, if 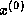 is very large
and very inaccurate, then
is very large
and very inaccurate, then  will be very large and
will be very large and  will be
artificially large; this means the iteration may stop too soon.
This criterion yields the forward error bound
will be
artificially large; this means the iteration may stop too soon.
This criterion yields the forward error bound
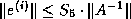 .
.





Next: When or is
Up: Stopping Criteria
Previous: Stopping Criteria
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
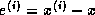 fall below a user-supplied threshold.
But
fall below a user-supplied threshold.
But 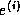 is hard to estimate directly, so
we use the residual
is hard to estimate directly, so
we use the residual 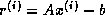 instead, which is
more readily computed. The rest of this section describes how to measure
the sizes of vectors
instead, which is
more readily computed. The rest of this section describes how to measure
the sizes of vectors 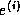 and
and  , and how to bound
, and how to bound 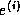 in terms of
in terms of  .
.

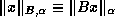 , where
, where 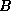 is a fixed nonsingular
matrix and
is a fixed nonsingular
matrix and  is one of
is one of 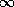 ,
,  , or
, or  .
Corresponding to these vector norms are three matrix norms:
.
Corresponding to these vector norms are three matrix norms:
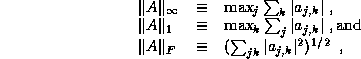
 .
We may also use the matrix norm
.
We may also use the matrix norm
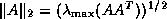 , where
, where  denotes the largest eigenvalue.
Henceforth
denotes the largest eigenvalue.
Henceforth  and
and 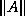 will refer to any mutually
consistent pair of the above.
(
will refer to any mutually
consistent pair of the above.
(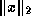 and
and  , as well as
, as well as 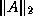 , both form
mutually consistent pairs.)
All these norms satisfy the triangle inequality
, both form
mutually consistent pairs.)
All these norms satisfy the triangle inequality  and
and 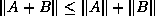 , as well as
, as well as  for mutually consistent pairs.
(For more details on the properties of norms, see Golub and
Van Loan
for mutually consistent pairs.
(For more details on the properties of norms, see Golub and
Van Loan  of length
of length  with entries uniformly distributed between
0 and 1 will satisfy
with entries uniformly distributed between
0 and 1 will satisfy 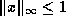 , but
, but  and
and 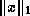 will grow like
will grow like  .
Since
.
Since  ,
which we will call the forward error,
is hard to estimate directly,
we introduce
the backward error, which allows us to bound the forward error.
The normwise backward error is defined as
the smallest possible value of
,
which we will call the forward error,
is hard to estimate directly,
we introduce
the backward error, which allows us to bound the forward error.
The normwise backward error is defined as
the smallest possible value of
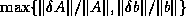 where
where
 is the exact solution of
is the exact solution of 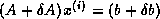 (here
(here 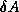 denotes a general matrix, not
denotes a general matrix, not  times
times  ; the
same goes for
; the
same goes for  ).
The backward error may be easily computed from the residual
).
The backward error may be easily computed from the residual
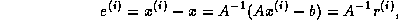
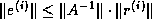 .
Therefore, a stopping criterion of the form ``stop when
.
Therefore, a stopping criterion of the form ``stop when  '' also yields an upper bound on the forward error
'' also yields an upper bound on the forward error
 . (Sometimes we may prefer to
use the stricter but harder to estimate bound
. (Sometimes we may prefer to
use the stricter but harder to estimate bound 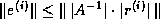 ; see §
; see § is the matrix or vector of absolute values of components of
is the matrix or vector of absolute values of components of
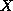 .)
.)
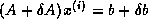 . If the original data
. If the original data 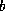 have
errors from previous computations or measurements,
then it is usually not worth iterating until
have
errors from previous computations or measurements,
then it is usually not worth iterating until  , it is not
worth making
, it is not
worth making  and
and
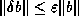 , because just rounding the entries
of
, because just rounding the entries
of 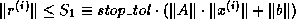 .
This is equivalent to asking that
the backward error
.
This is equivalent to asking that
the backward error  and
and
 .
This criterion yields the forward error bound
.
This criterion yields the forward error bound

 .
This is equivalent to asking that
the backward error
.
This is equivalent to asking that
the backward error 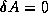 and
and 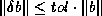 .
One difficulty with this method is that if
.
One difficulty with this method is that if 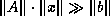 ,
which can only occur if
,
which can only occur if 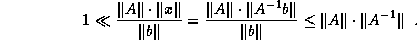

 is available, one can also just stop
when the upper bound on the error
is available, one can also just stop
when the upper bound on the error  falls below
a threshold. This yields the third stopping criterion:
falls below
a threshold. This yields the third stopping criterion:
 .
This stopping criterion guarantees that
.
This stopping criterion guarantees that
 and
and  measure each entry of
measure each entry of 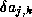 and
and 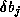 differently,
including the possibility of insisting that some entries be zero.
The cost is an extra matrix-vector multiply:
differently,
including the possibility of insisting that some entries be zero.
The cost is an extra matrix-vector multiply:
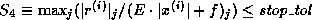 .
Here
.
Here  is a user-defined matrix of nonnegative entries,
is a user-defined matrix of nonnegative entries,
 is a user-defined vector of nonnegative entries, and
is a user-defined vector of nonnegative entries, and
 denotes the vector of absolute values of the entries of
denotes the vector of absolute values of the entries of  .
If this criterion is satisfied, it means there are a
.
If this criterion is satisfied, it means there are a 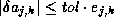 , and
, and
 for all
for all 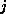 and
and  .
By choosing
.
By choosing 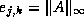 and
and 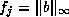 makes the stopping criterion
makes the stopping criterion
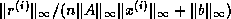 ,
which is essentially the same as Criterion 1. Choosing
,
which is essentially the same as Criterion 1. Choosing  and
and
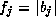 makes the stopping criterion measure the
componentwise relative backward error, i.e., the smallest relative
perturbations in any component of
makes the stopping criterion measure the
componentwise relative backward error, i.e., the smallest relative
perturbations in any component of 
 .
.
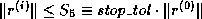 .
This commonly used criterion has the disadvantage of depending too strongly
on the initial solution
.
This commonly used criterion has the disadvantage of depending too strongly
on the initial solution 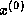 . If
. If  , a common choice, then
, a common choice, then
 . Then this criterion is equivalent to Criterion 2 above, which
may be difficult to satisfy for any algorithm
if
. Then this criterion is equivalent to Criterion 2 above, which
may be difficult to satisfy for any algorithm
if  .
On the other hand, if
.
On the other hand, if  will be very large and
will be very large and  will be
artificially large; this means the iteration may stop too soon.
This criterion yields the forward error bound
will be
artificially large; this means the iteration may stop too soon.
This criterion yields the forward error bound
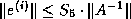 .
.