
The Poisson differential operator can be split in a natural way as the sum of two operators:

Now let 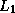 ,
, 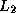 be discretized representations of
be discretized representations of  ,
, 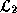 . Based on the observation that
. Based on the observation that
 , iterative schemes
such as
, iterative schemes
such as
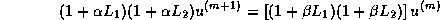
with suitable choices of  and
and  have been proposed.
have been proposed.
This alternating direction implicit, or ADI, method was first
proposed as a solution method for parabolic equations. The  are then approximations on subsequent time steps. However, it can also
be used for the steady state, that is, for solving elliptic equations.
In that case, the
are then approximations on subsequent time steps. However, it can also
be used for the steady state, that is, for solving elliptic equations.
In that case, the  become subsequent iterates;
see D'Yakonov [82],
Fairweather, Gourlay and Mitchell [97],
Hadjidimos [119], and
Peaceman and Rachford [173].
Generalization
of this scheme to variable coefficients or fourth order elliptic
problems is relatively straightforward.
become subsequent iterates;
see D'Yakonov [82],
Fairweather, Gourlay and Mitchell [97],
Hadjidimos [119], and
Peaceman and Rachford [173].
Generalization
of this scheme to variable coefficients or fourth order elliptic
problems is relatively straightforward.
The above method is implicit since it requires systems solutions, and it
alternates the  and
and 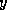 (and if necessary
(and if necessary  ) directions. It is
attractive from a practical point of view (although mostly on tensor
product grids), since solving a system with, for instance,
a matrix
) directions. It is
attractive from a practical point of view (although mostly on tensor
product grids), since solving a system with, for instance,
a matrix 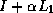 entails only a number of uncoupled tridiagonal
solutions. These need very little storage over that needed for the
matrix, and they can be executed in parallel , or one can vectorize
over them.
entails only a number of uncoupled tridiagonal
solutions. These need very little storage over that needed for the
matrix, and they can be executed in parallel , or one can vectorize
over them.
A theoretical reason that ADI preconditioners are of interest is that they can be shown to be spectrally equivalent to the original coefficient matrix. Hence the number of iterations is bounded independent of the condition number.
However, there is a problem of data distribution. For vector
computers, either the system solution with 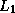 or with
or with 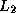 will
involve very large strides: if columns of variables in the grid are
stored contiguously, only the solution with
will
involve very large strides: if columns of variables in the grid are
stored contiguously, only the solution with 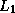 will involve
contiguous data. For the
will involve
contiguous data. For the 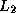 the stride equals the number of
variables in a column.
the stride equals the number of
variables in a column.
On parallel machines an efficient solution is possible if the
processors are arranged in a  grid. During, e.g., the
grid. During, e.g., the
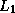 solve, every processor row then works independently of other
rows. Inside each row, the processors can work together, for instance
using a Schur complement method. With sufficient network bandwidth
this will essentially reduce the time
to that for solving any of the subdomain
systems plus the time for the interface system. Thus, this method will
be close to optimal.
solve, every processor row then works independently of other
rows. Inside each row, the processors can work together, for instance
using a Schur complement method. With sufficient network bandwidth
this will essentially reduce the time
to that for solving any of the subdomain
systems plus the time for the interface system. Thus, this method will
be close to optimal.