The convergence rate of iterative methods depends on spectral properties of the coefficient matrix. Hence one may attempt to transform the linear system into one that is equivalent in the sense that it has the same solution, but that has more favorable spectral properties. A preconditioner is a matrix that effects such a transformation.
For instance, if a matrix 
approximates the coefficient matrix 
in some way, the transformed system
has the same solution as the original system 
, but the spectral
properties of its coefficient matrix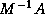 
may be more favorable.
In devising a preconditioner, we are faced with a choice between finding
a matrix that approximates , and for which solving a system is
easier than solving one with , or finding a matrix that
approximates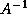 
, so that only multiplication by is needed.
The majority of preconditioners falls in the first category; a notable
example of the second category will be discussed in §
.