
Iterative methods are often used for solving discretized partial differential equations. In that context a rigorous analysis of the convergence of simple methods such as the Jacobi method can be given.
As an example, consider the boundary value problem

discretized by
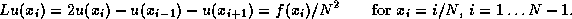
The eigenfunctions of the  and
and 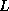 operator are the same:
for
operator are the same:
for 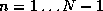 the function
the function 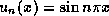 is an
eigenfunction corresponding to
is an
eigenfunction corresponding to  . The
eigenvalues of the Jacobi iteration matrix
. The
eigenvalues of the Jacobi iteration matrix 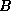 are then
are then
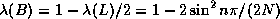 .
.
From this it is easy to see that the high frequency modes (i.e.,
eigenfunction 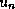 with
with  large) are damped quickly, whereas the
damping factor for modes with
large) are damped quickly, whereas the
damping factor for modes with  small is close to
small is close to  . The spectral
radius of the Jacobi iteration matrix is
. The spectral
radius of the Jacobi iteration matrix is
 , and it is attained for the eigenfunction
, and it is attained for the eigenfunction
 .
.
Spectral radius: The spectral radius of a matrix  is
is  .
Spectrum: The set of all eigenvalues of a matrix.
.
Spectrum: The set of all eigenvalues of a matrix.
The type of analysis applied to this example can be generalized to
higher dimensions and other stationary iterative methods. For both the
Jacobi and Gauss-Seidel method
(below) the spectral radius is found to be  where
where  is the
discretization mesh width, i.e.,
is the
discretization mesh width, i.e., 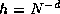 where
where  is the
number of variables and
is the
number of variables and  is the number of space dimensions.
is the number of space dimensions.