Blocked operations in the GMRES method





Next: Remaining topics
Up: Parallelism
Previous: Wavefronts in the
In addition to the usual matrix-vector product, inner products and
vector updates, the preconditioned GMRES method
(see § ) has a kernel where one new vector,
) has a kernel where one new vector,
 , is orthogonalized against the previously built
orthogonal set {
, is orthogonalized against the previously built
orthogonal set {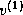 ,
, 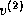 ,...,
,..., 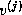 }.
In our version, this is
done using Level 1 BLAS, which may be quite inefficient. To
incorporate Level 2 BLAS we can apply either Householder
orthogonalization or classical Gram-Schmidt twice (which mitigates
classical Gram-Schmidt's potential instability; see
Saad [185]). Both
approaches significantly increase the computational work, but using
classical Gram-Schmidt has the advantage that all inner products can
be performed simultaneously; that is, their communication can be
packaged. This may increase the efficiency of the computation
significantly.
}.
In our version, this is
done using Level 1 BLAS, which may be quite inefficient. To
incorporate Level 2 BLAS we can apply either Householder
orthogonalization or classical Gram-Schmidt twice (which mitigates
classical Gram-Schmidt's potential instability; see
Saad [185]). Both
approaches significantly increase the computational work, but using
classical Gram-Schmidt has the advantage that all inner products can
be performed simultaneously; that is, their communication can be
packaged. This may increase the efficiency of the computation
significantly.
Another way to obtain more parallelism and
data locality is to generate a basis
{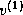 ,
,  , ...,
, ..., 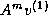 } for the Krylov subspace first,
and to orthogonalize this set afterwards; this is called
} for the Krylov subspace first,
and to orthogonalize this set afterwards; this is called
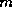 -step GMRES(
-step GMRES(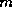 ) (see Kim and Chronopoulos [139]).
(Compare this to the GMRES method in §
) (see Kim and Chronopoulos [139]).
(Compare this to the GMRES method in § , where each
new vector is immediately orthogonalized to all previous vectors.)
This approach does not
increase the computational work and, in contrast to CG, the numerical
instability due to generating a possibly near-dependent set is not
necessarily a drawback.
, where each
new vector is immediately orthogonalized to all previous vectors.)
This approach does not
increase the computational work and, in contrast to CG, the numerical
instability due to generating a possibly near-dependent set is not
necessarily a drawback.
Jack Dongarra
Mon Nov 20 08:52:54 EST 1995
 , is orthogonalized against the previously built
orthogonal set {
, is orthogonalized against the previously built
orthogonal set {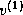 ,
, 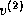 ,...,
,..., 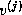 }.
In our version, this is
done using Level 1 BLAS, which may be quite inefficient. To
incorporate Level 2 BLAS we can apply either Householder
orthogonalization or classical Gram-Schmidt twice (which mitigates
classical Gram-Schmidt's potential instability; see
Saad [185]). Both
approaches significantly increase the computational work, but using
classical Gram-Schmidt has the advantage that all inner products can
be performed simultaneously; that is, their communication can be
packaged. This may increase the efficiency of the computation
significantly.
}.
In our version, this is
done using Level 1 BLAS, which may be quite inefficient. To
incorporate Level 2 BLAS we can apply either Householder
orthogonalization or classical Gram-Schmidt twice (which mitigates
classical Gram-Schmidt's potential instability; see
Saad [185]). Both
approaches significantly increase the computational work, but using
classical Gram-Schmidt has the advantage that all inner products can
be performed simultaneously; that is, their communication can be
packaged. This may increase the efficiency of the computation
significantly.
 , ...,
, ..., 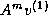 } for the Krylov subspace first,
and to orthogonalize this set afterwards; this is called
} for the Krylov subspace first,
and to orthogonalize this set afterwards; this is called
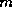 -step GMRES(
-step GMRES(