Notes

The appendix consists mainly of indexes giving the nearest LAPACK equivalents of LINPACK and EISPACK routines. These indexes should not be followed blindly or rigidly, especially when two or more LINPACK or EISPACK routines are being used together: in many such cases one of the LAPACK driver routines may be a suitable replacement.
When two or more LAPACK routines are given in a single entry, these routines must be combined to achieve the equivalent function.
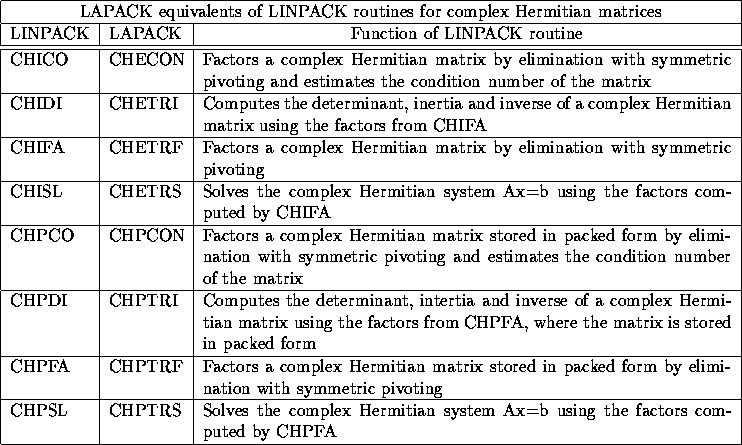
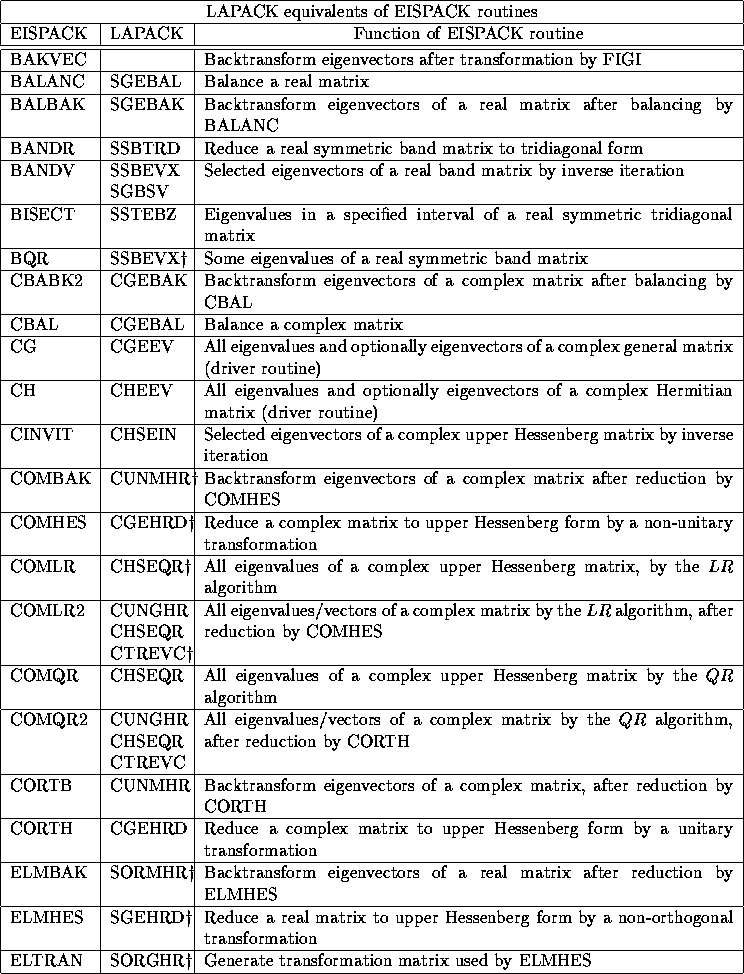
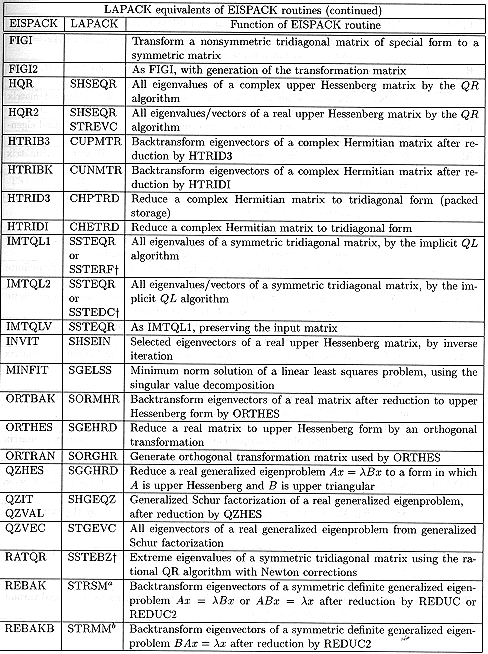
For LINPACK, an index is given for equivalents of the real LINPACK routines; these equivalences apply also to the corresponding complex routines. A separate table is included for equivalences of complex Hermitian routines. For EISPACK, an index is given for all real and complex routines, since there is no direct 1-to-1 correspondence between real and complex routines in EISPACK.
A few of the less commonly used routines in LINPACK and EISPACK have no equivalents in Release 1.0 of LAPACK; equivalents for some of these (but not all) are planned for a future release.
For some EISPACK routines, there are LAPACK routines providing similar functionality, but using a significantly different method, or LAPACK routines which provide only part of the functionality; such routines are marked by a . For example, the EISPACK routine ELMHES uses non-orthogonal transformations, whereas the nearest equivalent LAPACK routine, SGEHRD, uses orthogonal transformations.
In some cases the LAPACK equivalents require matrices to be stored in a different storage scheme. For example:
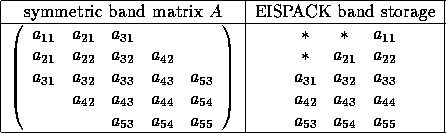
- EISPACK routines BANDR , BANDV , BQR and the driver routine RSB require the lower triangle of a symmetric band matrix to be stored in a different storage scheme to that used in LAPACK, which is illustrated in subsection 5.3.3. The corresponding storage scheme used by the EISPACK routines is:
- EISPACK routines TRED1 , TRED2 , TRED3 , HTRID3 , HTRIDI , TQL1 , TQL2 , IMTQL1 , IMTQL2 , RATQR , TQLRAT and the driver routine RST store the off-diagonal elements of a symmetric tridiagonal matrix in elements 2 : n of the array E, whereas LAPACK routines use elements 1 : n - 1.
The EISPACK and LINPACK routines for the singular value decomposition return the matrix of right singular vectors, V, whereas the corresponding LAPACK routines return the transposed matrix .
In general, the argument lists of the LAPACK routines are different from those of the corresponding EISPACK and LINPACK routines, and the workspace requirements are often different.

   LAPACK equivalents of LINPACK routines for real matrices
----------------------------------------------------------------
LINPACK  LAPACK   Function of LINPACK routine
----------------------------------------------------------------
SCHDC             Cholesky factorization with diagonal pivoting
                  option
----------------------------------------------------------------
SCHDD             rank-1 downdate of a Cholesky factorization
                  or the triangular factor of a QR factorization
----------------------------------------------------------------
SCHEX             rank-1 update of a Cholesky factorization
                  or the triangular factor of a QR factorization
----------------------------------------------------------------
SCHUD              modifies a Cholesky factorization under
                   permutations of the original matrix
----------------------------------------------------------------
SGBCO    SLANGB    LU factorization and condition estimation
         SGBTRF    of a general band matrix
         SGBCON
----------------------------------------------------------------
SGBDI              determinant of a general band matrix,
                   after factorization by SGBCO or SGBFA
----------------------------------------------------------------
SGBFA    SGBTRF    LU factorization of a general band matrix
----------------------------------------------------------------
SGBSL    SGBTRS    solves a general band system of linear
                   equations, after factorization by SGBCO
                   or SGBFA
----------------------------------------------------------------
SGECO    SLANGE    LU factorization and condition
         SGETRF    estimation of a general matrix
         SGECON
----------------------------------------------------------------
SGEDI    SGETRI    determinant and inverse of a general
                   matrix, after factorization by SGECO
                   or SGEFA
----------------------------------------------------------------
SGEFA    SGETRF    LU factorization of a general matrix
----------------------------------------------------------------
SGESL    SGETRS    solves a general system of linear
                   equations, after factorization by
                   SGECO or SGEFA
----------------------------------------------------------------
SGTSL    SGTSV     solves a general tridiagonal system
                   of linear equations
----------------------------------------------------------------
SPBCO    SLANSB    Cholesky factorization and condition
         SPBTRF    estimation of a symmetric positive definite
         SPBCON    band matrix
----------------------------------------------------------------
SPBDI              determinant of a symmetric positive
                   definite band matrix, after factorization
                   by SPBCO or SPBFA
----------------------------------------------------------------
SPBFA    SPBTRF    Cholesky factorization of a symmetric
                   positive definite band matrix
----------------------------------------------------------------
SPBSL    SPBTRS    solves a symmetric positive definite band
                   system of linear equations, after
                   factorization by SPBCO or SPBFA
----------------------------------------------------------------
SPOCO    SLANSY    Cholesky factorization and condition
         SPOTRF    estimation of a symmetric positive definite
         SPOCON    matrix
----------------------------------------------------------------
SPODI    SPOTRI    determinant and inverse of a symmetric
                   positive definite matrix, after factorization
                   by SPOCO or SPOFA
----------------------------------------------------------------
SPOFA    SPOTRF    Cholesky factorization of a symmetric
                   positive definite matrix
----------------------------------------------------------------
SPOSL    SPOTRS    solves a symmetric positive definite system
                   of linear equations, after factorization by
                   SPOCO or SPOFA
----------------------------------------------------------------
SPPCO    SLANSY    Cholesky factorization and condition
         SPPTRF    estimation of a symmetric positive definite
         SPPCON    matrix (packed storage)
----------------------------------------------------------------

               LAPACK equivalents of LINPACK
            routines for real matrices(continued)
----------------------------------------------------------------
LINPACK  LAPACK    Function of LINPACK routine}\\
----------------------------------------------------------------
SPPDI    SPPTRI    determinant and inverse of a symmetric
                   positive definite matrix, after factorization
                   by SPPCO or SPPFA (packed storage)
----------------------------------------------------------------
SPPFA    SPPTRF    Cholesky factorization of a symmetric
                   positive definite matrix (packed storage)
----------------------------------------------------------------
SPPSL    SPPTRS    solves a symmetric positive definite system
                   of linear equations, after factorization by
                   SPPCO or SPPFA (packed storage)
----------------------------------------------------------------
SPTSL    SPTSV     solves a symmetric positive definite
                   tridiagonal system of linear equations
----------------------------------------------------------------
SQRDC    SGEQPF    QR factorization with optional column
         or        pivoting
         SGEQRF
----------------------------------------------------------------
SQRSL    SORMQR    solves linear least squares problems after
         STRSV     factorization by SQRDC
----------------------------------------------------------------
SSICO    SLANSY    symmetric indefinite factorization and
         SSYTRF    condition estimation of a symmetric
         SSYCON    indefinite matrix
----------------------------------------------------------------
SSIDI    SSYTRI    determinant, inertia and inverse of a
                   symmetric indefinite matrix, after
                   factorization by SSICO or SSIFA
----------------------------------------------------------------
SSIFA    SSYTRF    symmetric indefinite factorization of a
                   symmetric indefinite matrix
----------------------------------------------------------------
SSISL    SSYTRS    solves a symmetric indefinite system of
                   linear equations, after factorization by
                   SSICO or SSIFA
----------------------------------------------------------------
SSPCO    SLANSP    symmetric indefinite factorization and
         SSPTRF    condition estimation of a symmetric
         SSPCON    indefinite matrix (packed storage)
----------------------------------------------------------------
SSPDI    SSPTRI    determinant, inertia and inverse of a
                   symmetric indefinite matrix, after
                   factorization by SSPCO or SSPFA (packed
                   storage)
----------------------------------------------------------------
SSPFA    SSPTRF    symmetric indefinite factorization of a
                   symmetric indefinite matrix (packed storage)
----------------------------------------------------------------
SSPSL    SSPTRS    solves a symmetric indefinite system of
                   linear equations, after factorization by
                   SSPCO or SSPFA (packed storage)
----------------------------------------------------------------
SSVDC    SGESVD    all or part of the singular value
                   decomposition of a general matrix
----------------------------------------------------------------
STRCO    STRCON    condition estimation of a triangular matrix
----------------------------------------------------------------
STRDI    STRTRI    determinant and inverse of a triangular
                   matrix
----------------------------------------------------------------
STRSL    STRTRS    solves a triangular system of linear
                   equations
----------------------------------------------------------------

Next: LAPACK Working Notes Up: Converting from LINPACK Previous: Converting from LINPACK

Tue Nov 29 14:03:33 EST 1994