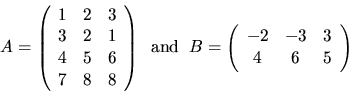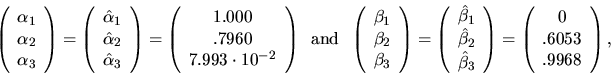The generalized (or quotient) singular value decomposition
of an m-by-n matrix
A and a p-by-n matrix B is the pair of factorizations
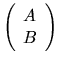 ,
and satisfies
,
and satisfies
The generalized singular value decomposition is
computed by driver routine xGGSVD (see section 2.3.5.3).
We will give error bounds for the generalized
singular values in the
common case where
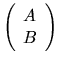 has full
rank r=n.
Let
has full
rank r=n.
Let
![]() and
and ![]() be the values of
be the values of ![]() and
and ![]() ,
respectively,
computed by xGGSVD.
The approximate error
bound4.10for these values is
,
respectively,
computed by xGGSVD.
The approximate error
bound4.10for these values is
Here is another way to interpret SERRBD:
if we think of ![]() and
and ![]() as representing the subspace
as representing the subspace ![]() consisting of the straight line through the origin with slope
consisting of the straight line through the origin with slope
![]() ,
and similarly
,
and similarly
![]() and
and ![]() representing the subspace
representing the subspace ![]() ,
then
,
then ![]() bounds the acute angle between
bounds the acute angle between
![]() and
and ![]() .
Note that any two
lines through the origin with nearly vertical slopes
(very large
.
Note that any two
lines through the origin with nearly vertical slopes
(very large
![]() )
are close together in angle.
(This is related to the chordal distance in
section 4.10.1.)
)
are close together in angle.
(This is related to the chordal distance in
section 4.10.1.)
SERRBD can be computed by the following code fragment,
which for simplicity assumes ![]() .
(The assumption r=n implies only that
.
(The assumption r=n implies only that ![]() .
Error bounds can also be computed when
.
Error bounds can also be computed when
![]() ,
with slightly more complicated code.)
,
with slightly more complicated code.)
EPSMCH = SLAMCH( 'E' )
* Compute generalized singular values of A and B
CALL SGGSVD( 'N', 'N', 'N', M, N, P, K, L, A, LDA, B,
$ LDB, ALPHA, BETA, U, LDU, V, LDV, Q, LDQ,
$ WORK, IWORK, INFO )
* Compute rank of [A',B']'
RANK = K+L
IF( INFO.GT.0 ) THEN
PRINT *,'SGGSVD did not converge'
ELSE IF( RANK.LT.N ) THEN
PRINT *,'[A**T,B**T]**T not full rank'
ELSE IF ( M .GE. N .AND. N .GT. 0 ) THEN
* Compute reciprocal condition number RCOND of R
CALL STRCON( 'I', 'U', 'N', N, A, LDA, RCOND, WORK, IWORK,
$ INFO )
RCOND = MAX( RCOND, EPSMCH )
SERRBD = EPSMCH / RCOND
END IF
For example4.11, if
![]() ,
,