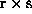We model only the inner loop of the IFS code which takes the major part of the
runtime for large examples. We consider a 2D partitioning of the 3D spaces
where a structure of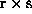 
processes of nearly identical size is
produced. The current partitioning of the RAPS-2.0 code is roughly described in
section 4 (cf. [3]).
We consider only those cases where the number of computing nodes of the cluster
equals the number of processes (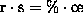 
). The inner loop consists of six computational steps separated by
transpositions of the space. The transpositions are required to provide just
that dimension of the space unsplit which is entirely requested for the current
computational step. These transpositions mainly consist of data exchange where
all processes of a row or column of our 2D process structure send a message to
all other processes of the same row or column respectively. Since some of the
exchange phases are very short when containing intra-system transfer only and
because of data dependences, we can observe a series-parallel behaviour. As a
consequence, we can model the total
runtime of the inner loop approximately by a sum of runtimes of subsequent
calculation or communication phases:
where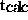 
represents the computing time and 
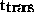the
transposition time. These functions are approximately determined by
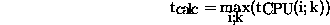
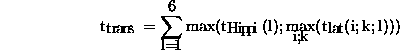
where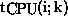 
is the calculation time of process (i,k), 
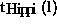is the maximum time cost needed by one of the Hippi channels for all related
messages, and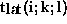 
is the time cost of a processor for all messages
of process (i,k) that are transported via the Hippi channel during
transposition l (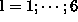 
). The time cost for buffering data before or
after the transfer and the intra-system communication has for simplicity been
suppressed in our description. These time costs had been considered in the
actual modelling additionally. But they turned out to be so small that they
could not be shown in the graphical representation of results. For the
model evaluation, we used a special tool [6].
To calculate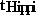 
, we used the Hippi transfer parameters (0.02 ms/kbyte
and 0.46 ms/start) and the actual message numbers and sizes from corresponding
IFS runs.
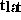is calculated considering the messages of single processes using the
parameters 0.07 ms/kbyte and 1.46 ms/start.
To estimate 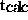, we assume that processes of the parallel IFS show nearly
the same computational work if they are identical in size and shape.
The sequential IFS and the parallel message passing version of IFS were
measured on a single C90 system using resolutions up to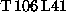 
.
We used the standard timing values produced by the
considered code. These are mainly total time, Legendre transform, inverse
Legendre transform, Fourier space calculations together with FFT and inverse
FFT, and spectral space calculations.
We developed approximative complexity formulas for four different computational parts: grid point space calculations, FFT, Legendre transform, and spectral space calculations. The grid point space calculations represent the most important part of the computational work. For the majority of calculations it is in principle possible to integrate all grid points of a single level in one vector operation [3]. This way of vectorisation is considered a best case model. It is used to obtain our main result. For more details we refer to [7].
Based on 45 sets of measurements on 1 to 8 processors, we determined the
following approximative expression for the computational work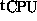 
:
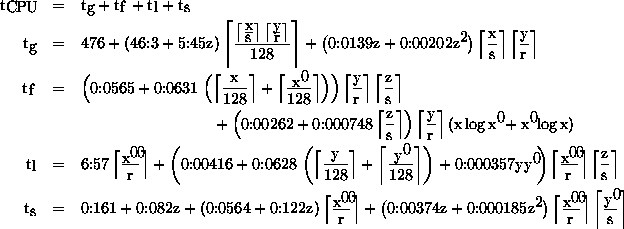
where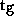 
, 
, 
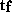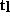, and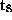 
represent calculations in the grid
point space, during FFT, during Legendre transform, or in the spectral space
respectively. In relation to the problem size TM Lz, the variables are
defined by
, 
,
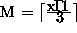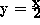x'=M+1, 
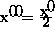, and y'=x'+1. All parameters are in
ms. The start-up time of the vector unit is modelled by terms showing 128 as
denominator. The deviation of the estimated values from measurements was in
general less than 10%.
As an alternative worst case model, we also used vectorisation in direction of longitudes or latitudes only from one boundary to the opposite boundary. Since the C90 hardware does not allow to start vector operations for more than 128 elements at once, there is no big difference between our models in the case of large examples. For small examples, however, or in the case of very fine partitioning to many parallel processes, the worst case model delivered runtime values which were higher than those of the best case model by 10 to 20%. Since this effect is observed for 16 processors of a single system as well as for the 32 or 64 processors of a cluster, there was no big difference in terms of cluster efficiency. Therefore, we decided to discuss the best case model only throughout this paper.
