Both spectral divide and conquer (SDC) algorithms discussed in this paper can be presented in the following framework. Let
be the Jordan canonical form of 
, where the eigenvalues of the 
submatrix 
are the eigenvalues of inside a
selected region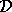 
in the complex plane,
and the eigenvalues of the
submatrix 
are the eigenvalues of outside .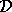
We assume that there are no eigenvalues of on the boundary
of 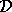, otherwise we reselect or move the region 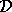slightly.
The invariant subspace of the matrix corresponding to the
eigenvalues inside 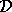are spanned
by the first 
columns of 
. The matrix
is the corresponding spectral projector.
Let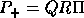 
be the rank revealing QR decomposition of the
matrix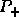 
, where 
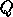is unitary, 
is upper triangular,
and 
is a permutation matrix chosen
so that the leading columns of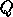
span the range space of 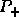. Then 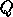yields the desired spectral
decomposition:
where the eigenvalues of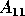 
are the eigenvalues of inside
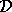, and the eigenvalues of 
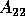are the
eigenvalues of outside .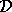
By substituting the complementary projector 
for 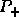in (2.4),
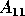will have the eigenvalues outside 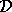and
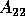will have the eigenvalues inside .
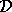The crux of a parallel SDC algorithm is to efficiently
compute the desired spectral projector 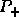without
computing the Jordan canonical form.
